What is (x^2y^-2)^3?
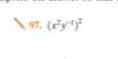
Understand the Problem
The question is presenting a mathematical expression, specifically a comparison or question regarding the expression (x^2y^-2)^3. The goal likely involves simplifying this expression or analyzing its properties.
Answer
The simplified expression is $$ \frac{x^{6}}{y^{6}} $$.
Answer for screen readers
The simplified expression is $$ \frac{x^{6}}{y^{6}} $$.
Steps to Solve
- Apply the Power of a Power Rule
When raising a power to a power, multiply the exponents. Here, we'll apply this rule to each factor in the expression:
$$(x^2y^{-2})^{3} = (x^2)^{3}(y^{-2})^{3}$$
- Simplify Each Factor
Now, simplify each power:
$$(x^2)^{3} = x^{2 \cdot 3} = x^{6}$$
$$(y^{-2})^{3} = y^{-2 \cdot 3} = y^{-6}$$
- Combine the Results
Combining the results gives:
$$ (x^2y^{-2})^{3} = x^{6}y^{-6} $$
Alternatively, we can write this as:
$$ \frac{x^{6}}{y^{6}} $$
The simplified expression is $$ \frac{x^{6}}{y^{6}} $$.
More Information
The expression $(x^2y^{-2})^{3}$ simplifies to $$ \frac{x^{6}}{y^{6}} $$ using the power of a power rule in exponents. This rule states that when you have a power raised to another power, you multiply the exponents.
Tips
- Neglecting to multiply exponents: A common mistake is to add the exponents instead of multiplying them when using the power of a power rule. To avoid this, always remember to multiply the exponent by the outer exponent.
- Forgetting to handle negative exponents correctly: Some might overlook that $y^{-6}$ can be written as $\frac{1}{y^{6}}$. It's helpful to rewrite negative exponents as fractions for clarity.
AI-generated content may contain errors. Please verify critical information