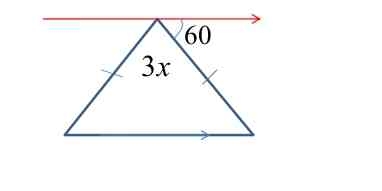
What is the value of x in the triangle where one angle is 60 degrees and another is 3x?
Understand the Problem
The question involves a triangle where two of the angles are given in terms of a variable (3x and 60 degrees). We likely need to solve for the variable x, potentially using the property that the sum of the interior angles of a triangle is 180 degrees.
Answer
There are infinite values for $x$.
Answer for screen readers
There are infinite values for $x$ that satisfy the triangle's angle condition.
Steps to Solve
- Set up the angle equation
The sum of the interior angles in a triangle equals 180 degrees.
The angles are $3x$, $60^\circ$, and the third angle can be represented as $(180 - 3x - 60)$.
- Write the equation for the angles
Using the angle sum property, we have: $$ 3x + 60 + (180 - 3x - 60) = 180 $$
- Simplify the equation
Combine like terms: $$ 3x + 60 + 180 - 3x - 60 = 180 $$
This simplifies to: $$ 180 = 180 $$
- Finding the value of x
Notice that the $3x$ terms cancel each other out, leading to an identity. This means the variable $x$ can take any value that satisfies the conditions of a triangle.
- Conclusion on x
Since the angles sum up correctly for all values of $x$, any valid value of $x$ will lead to valid triangle angles, as the triangle conditions remain intact.
There are infinite values for $x$ that satisfy the triangle's angle condition.
More Information
In this case, because the equation simplifies to a true statement (180 = 180), it shows the relation between the angles allows for flexibility in the variable $x$. All values of $x$ yield angle measures that still conform to the triangle sum property.
Tips
null
AI-generated content may contain errors. Please verify critical information