What is the value of x in \frac{9}{7} - x = \frac{2}{3}?
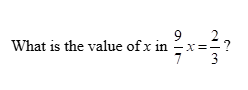
Understand the Problem
The question is asking to find the value of x in the equation involving fractions. We need to isolate x to determine its value.
Answer
The value of $x$ is $\frac{13}{21}$.
Answer for screen readers
The value of $x$ is $\frac{13}{21}$.
Steps to Solve
- Rearranging the Equation
To isolate $x$, we need to add $x$ to both sides of the equation:
$$ \frac{9}{7} - x + x = \frac{2}{3} + x $$
This simplifies to:
$$ \frac{9}{7} = \frac{2}{3} + x $$
- Isolating x
Now, subtract $\frac{2}{3}$ from both sides to solve for $x$:
$$ x = \frac{9}{7} - \frac{2}{3} $$
- Finding a Common Denominator
The denominators are 7 and 3. The least common denominator (LCD) is 21. Convert each fraction:
$$ \frac{9}{7} = \frac{9 \cdot 3}{7 \cdot 3} = \frac{27}{21} $$
$$ \frac{2}{3} = \frac{2 \cdot 7}{3 \cdot 7} = \frac{14}{21} $$
- Subtract the Fractions
Now we can subtract the fractions:
$$ x = \frac{27}{21} - \frac{14}{21} = \frac{27 - 14}{21} = \frac{13}{21} $$
The value of $x$ is $\frac{13}{21}$.
More Information
The answer $\frac{13}{21}$ is a simplified fraction that represents the difference between the two fractions in the original equation.
Tips
- Forgetting to find a common denominator when subtracting fractions can lead to incorrect calculations. Always ensure to convert fractions to the same denominator before performing operations.
- Neglecting to isolate $x$ correctly can result in errors; keep track of your algebraic manipulations carefully.
AI-generated content may contain errors. Please verify critical information