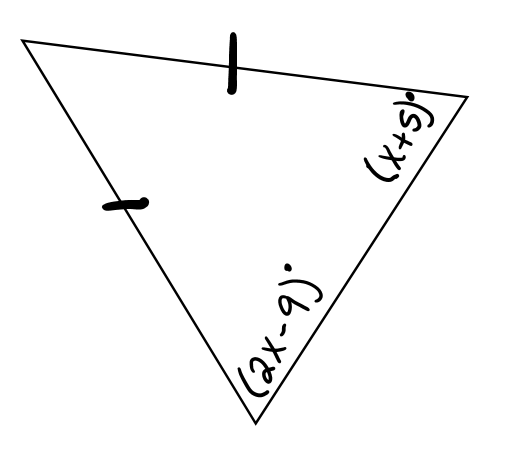
What is the value of x if the angles of the triangle are (2x - 9) and (x + 5)?

Steps to Solve

1. Set up the equation for the angles of the triangle

The sum of the angles in a triangle is always 180 degrees. We are given two angles: $(2x - 9)$ and $(x + 5)$. We can represent the sum of these two angles plus the third angle (which we'll denote as $A$) as:

$$ (2x - 9) + (x + 5) + A = 180 $$

2. Express the third angle

Since the problem does not specify the third angle directly, we can denote it as $A$. However, without additional information on $A$, we will assume it can be expressed in terms of $x$ or assume it's the third angle, which can also be a variable.

For simplicity, let's substitute known values later.

3. Combine the known angles

Combine the first two angles:

$$ (2x - 9) + (x + 5) = 3x - 4 $$

4. Set up the final equation

We can express the final equation as:

$$ (3x - 4) + A = 180 $$

And thus we can write:

$$ 3x - 4 + A = 180 $$

Assuming $A$ can be derived, you'd set $A = 180 - (3x - 4)$.

5. Solve for x considering angles

Let’s look only at the two angles we have:

$$ (2x - 9) + (x + 5) = 180 $$

Subtract $(x + 5)$ from both sides:

$$ 2x - 9 + x + 5 = 180 $$

Combine terms:

$$ 3x - 4 = 180 $$

6. Isolate 'x'

Add 4 to both sides:

$$ 3x = 184 $$

Now, divide by 3:

$$ x = \frac{184}{3} $$

Calculating this gives:

$$ x \approx 61.33 $$ (This is the assumed approach without specifying A)