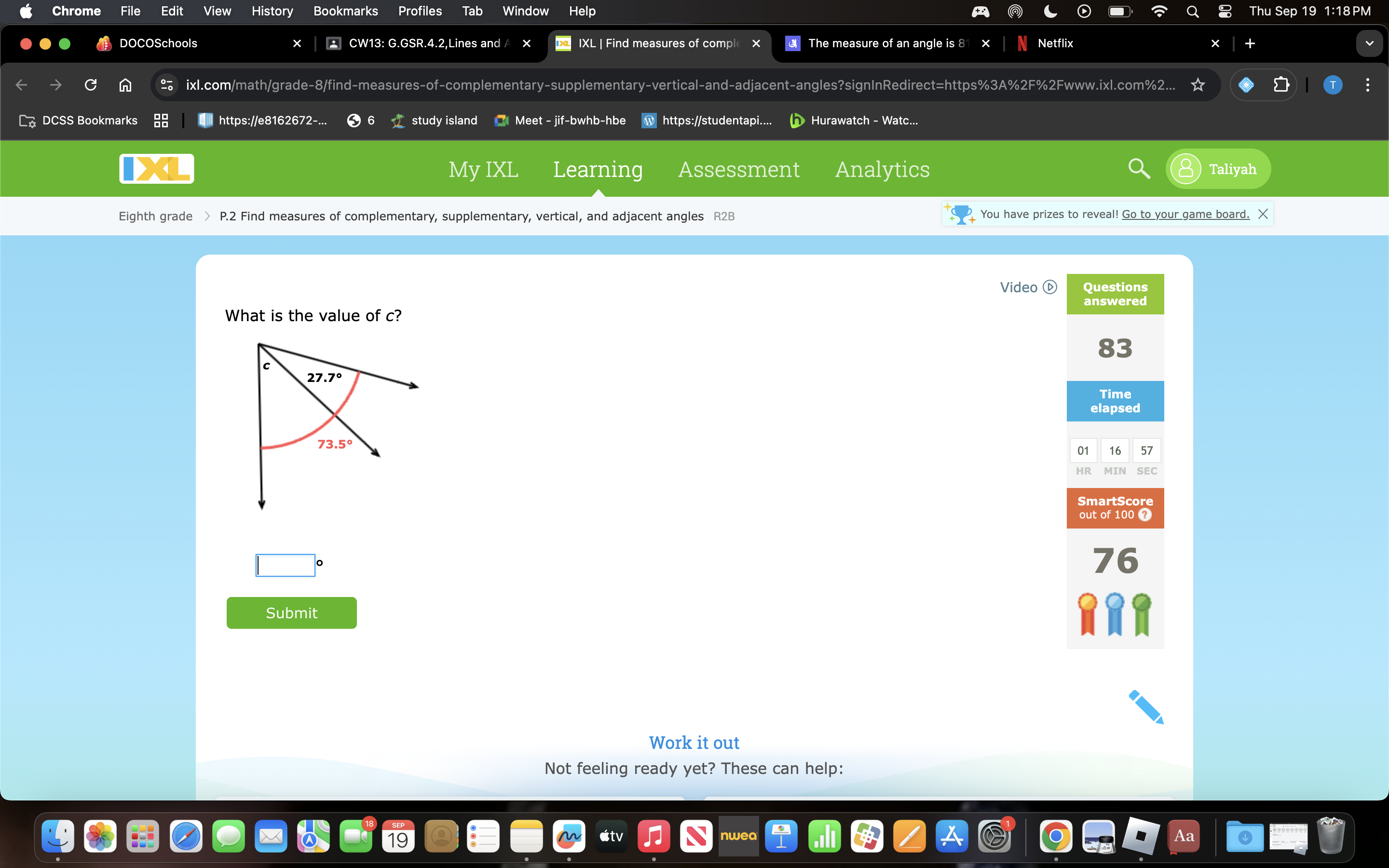
What is the value of c?
Understand the Problem
The question asks for the value of angle c given the measures of two angles: 27.7° and 73.5°. To find c, we need to utilize the property that angles on a straight line sum up to 180°.
Answer
The value of angle $c$ is $78.8^\circ$.
Answer for screen readers
The value of angle $c$ is $78.8^\circ$.
Steps to Solve
- Identify the known angles
We have two angles: $27.7^\circ$ and $73.5^\circ$.
- Use the linear angle relationship
We know that angles on a straight line sum up to $180^\circ$. Therefore, we can express this with the equation:
$$ c + 27.7^\circ + 73.5^\circ = 180^\circ $$
- Combine the known angles
Calculate the sum of the two known angles:
$$ 27.7^\circ + 73.5^\circ = 101.2^\circ $$
- Substitute and solve for c
Now substitute the sum back into the equation:
$$ c + 101.2^\circ = 180^\circ $$
To isolate $c$, subtract $101.2^\circ$ from both sides:
$$ c = 180^\circ - 101.2^\circ $$
- Final calculation
Now perform the subtraction:
$$ c = 78.8^\circ $$
The value of angle $c$ is $78.8^\circ$.
More Information
This problem demonstrates the concept of supplementary angles, which are pairs of angles that add up to $180^\circ$. In this case, $c$, along with the two other angles, fulfills this property.
Tips
- Forgetting to add the known angles before subtracting from 180°.
- Mixing up the angles; ensure you are only working with the angles on the same line.
AI-generated content may contain errors. Please verify critical information