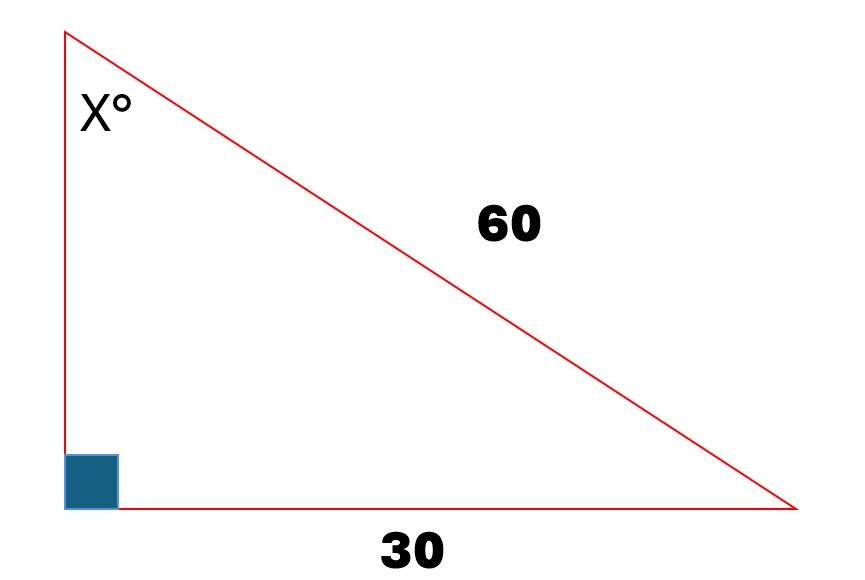
What is the value of angle X in the triangle with a 60° angle and side lengths of 30 and 60?
Understand the Problem
The question is asking to find the value of angle X in a right triangle where one angle is given as 60 degrees, and the sides opposite and adjacent are labeled with specific lengths. The user needs to apply the properties of triangles to find angle X.
Answer
$X = 30^\circ$
Answer for screen readers
The value of angle $X$ is $30^\circ$.
Steps to Solve
- Identify the Triangle Properties
In any triangle, the sum of the interior angles is always $180^\circ$. Here, we have one right angle ($90^\circ$) and one angle given as $60^\circ$.
- Set Up the Angle Equation
Using the property mentioned, we can set up the following equation for the angles: $$ 90^\circ + 60^\circ + X^\circ = 180^\circ $$
- Solve for Angle X
Now, simplify the equation: $$ X^\circ = 180^\circ - 90^\circ - 60^\circ $$
- Calculate the Value of X
Perform the calculation: $$ X^\circ = 180^\circ - 150^\circ = 30^\circ $$
The value of angle $X$ is $30^\circ$.
More Information
In a right triangle, the presence of a $90^\circ$ angle and another angle sums up to determine the third angle. These relationships are foundational in trigonometry and help in solving various problems involving triangles.
Tips
- Forgetting that the sum of angles in a triangle is $180^\circ$ or that each right triangle has one angle of $90^\circ$.
- Miscalculating the angles by overlooking the subtraction process; carefully following each step helps avoid this.