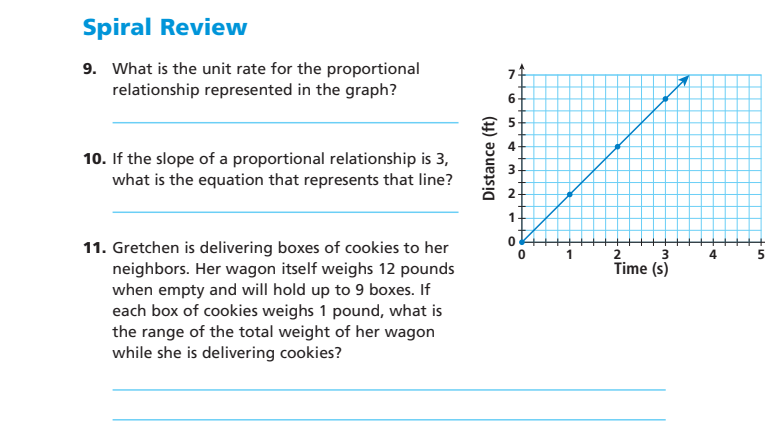
What is the unit rate for the proportional relationship represented in the graph? If the slope of a proportional relationship is 3, what is the equation that represents that line?... What is the unit rate for the proportional relationship represented in the graph? If the slope of a proportional relationship is 3, what is the equation that represents that line? What is the range of the total weight of Gretchen's wagon while she is delivering cookies?
Understand the Problem
The question is asking about the concepts of proportional relationships in mathematics. It includes determining the unit rate from a graph, finding an equation based on slope, and calculating the total weight of a wagon while delivering cookies based on given conditions.
Answer
The unit rate is $1.4$ ft/s, the equation is $y = 3x$, and the weight range is $12$ to $21$ pounds.
Answer for screen readers
-
The unit rate is $1.4$ feet per second.
-
The equation representing the line is $y = 3x$.
-
The range of the total weight of the wagon is from $12$ to $21$ pounds.
Steps to Solve
- Unit Rate from the Graph
First, look at the line in the graph. The unit rate represents the change in distance per change in time.
From the graph, it shows that when $x = 5$ seconds, $y = 7$ feet. To find the unit rate:
Calculate the slope (rise/run): $$ \text{slope} = \frac{7 - 0}{5 - 0} = \frac{7}{5} = 1.4 \text{ ft/s} $$
Thus, the unit rate is 1.4 feet per second.
- Equation of the Line with a Slope of 3
Given a slope of 3, the equation of a line in slope-intercept form is:
$$ y = mx + b $$
Where $m$ is the slope and $b$ is the y-intercept, which is 0 for a proportional relationship. Therefore, the equation becomes:
$$ y = 3x $$
- Total Weight of the Wagon while Delivering Cookies
The wagon weighs 12 pounds when empty, and can hold up to 9 boxes of cookies.
Each box weighs 1 pound, so for 0 to 9 boxes, the total weight $W$ can be calculated as:
$$ W = 12 + x $$
Where $x$ is the number of boxes.
The range of $x$ is 0 to 9, so the total weight ranges from:
-
When $x = 0$: $$ W = 12 + 0 = 12 \text{ pounds} $$
-
When $x = 9$: $$ W = 12 + 9 = 21 \text{ pounds} $$
The range of the total weight is from 12 to 21 pounds.
-
The unit rate is $1.4$ feet per second.
-
The equation representing the line is $y = 3x$.
-
The range of the total weight of the wagon is from $12$ to $21$ pounds.
More Information
The unit rate is a way to show how much distance is covered over a specific time, portraying the speed. The equation of a line describes the relationship between two proportional quantities. Understanding the total weight while adding boxes allows for practical applications in everyday scenarios, such as delivery logistics.
Tips
- Confusing slope with y-intercept; remember that the slope indicates steepness and the y-intercept is the starting point.
- Not correctly accounting for both empty and added weights when calculating the total weight.
- Misinterpreting the graph; ensure you are reading the axes correctly to find the unit rate.
AI-generated content may contain errors. Please verify critical information