Find all real and imaginary solutions to the equation x^3 - 7x^2 - 25x + 175 = 0
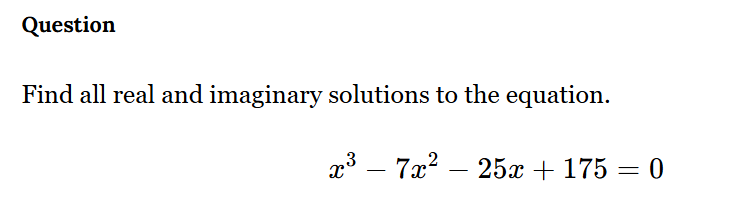
Understand the Problem
The question is asking us to find all real and imaginary solutions to a cubic equation. This involves identifying the roots of the polynomial and may require methods such as factoring, using the Rational Root Theorem, or applying the cubic formula.
Answer
The solutions are $x = 7, x = 5, x = -5$.
Answer for screen readers
The solutions to the equation $x^3 - 7x^2 - 25x + 175 = 0$ are:
$$ x = 7, x = 5, x = -5 $$
Steps to Solve
- Identify the equation The given equation is a cubic polynomial:
$$ x^3 - 7x^2 - 25x + 175 = 0 $$
- Use the Rational Root Theorem To find possible rational roots, list factors of the constant term (175) and the leading coefficient (1). The possible rational roots are:
$$ \pm 1, \pm 5, \pm 7, \pm 25, \pm 35, \pm 175 $$
- Testing possible roots We can start testing these possible roots in the original equation.
Testing $x = 7$:
$$ 7^3 - 7(7^2) - 25(7) + 175 = 343 - 343 - 175 + 175 = 0 $$
So, $x = 7$ is a root.
- Factor the polynomial Now, we can divide the cubic polynomial by $(x - 7)$ using synthetic division or polynomial long division.
Performing synthetic division with $7$ gives:
$$ x^2 + 0x - 25 $$
- Write the factored form The polynomial can now be rewritten as:
$$ (x - 7)(x^2 - 25) = 0 $$
- Solve the quadratic factor Now, solve the quadratic equation:
$$ x^2 - 25 = 0 $$
This factors as:
$$ (x - 5)(x + 5) = 0 $$
-
Find all solutions Setting each factor to zero gives the solutions:
-
$x - 7 = 0 \implies x = 7$
-
$x - 5 = 0 \implies x = 5$
-
$x + 5 = 0 \implies x = -5$
Thus, the solutions are:
$$ x = 7, x = 5, x = -5 $$
The solutions to the equation $x^3 - 7x^2 - 25x + 175 = 0$ are:
$$ x = 7, x = 5, x = -5 $$
More Information
These solutions are all real numbers; there are no imaginary solutions in this case. The factorization of a cubic polynomial typically helps in finding the roots efficiently, and recognizing that the quadratic factor created is simple to solve is key.
Tips
- Forgetting the Rational Root Theorem: Sometimes, students may skip listing all possible rational roots, which is crucial for identifying roots.
- Incorrect synthetic division: It’s important to ensure that the division is set up correctly; errors here can lead to wrong factors.
- Misinterpreting solutions of the quadratic: Some might overlook that $x^2 - 25$ is a difference of squares, potentially missing the two roots.
AI-generated content may contain errors. Please verify critical information