What is the total work W_{F2} done on the box by the applied force in this case? Express your answer in terms of any or all of the variables \, \mu, m, g, \theta, L, and F_{2}.
Understand the Problem
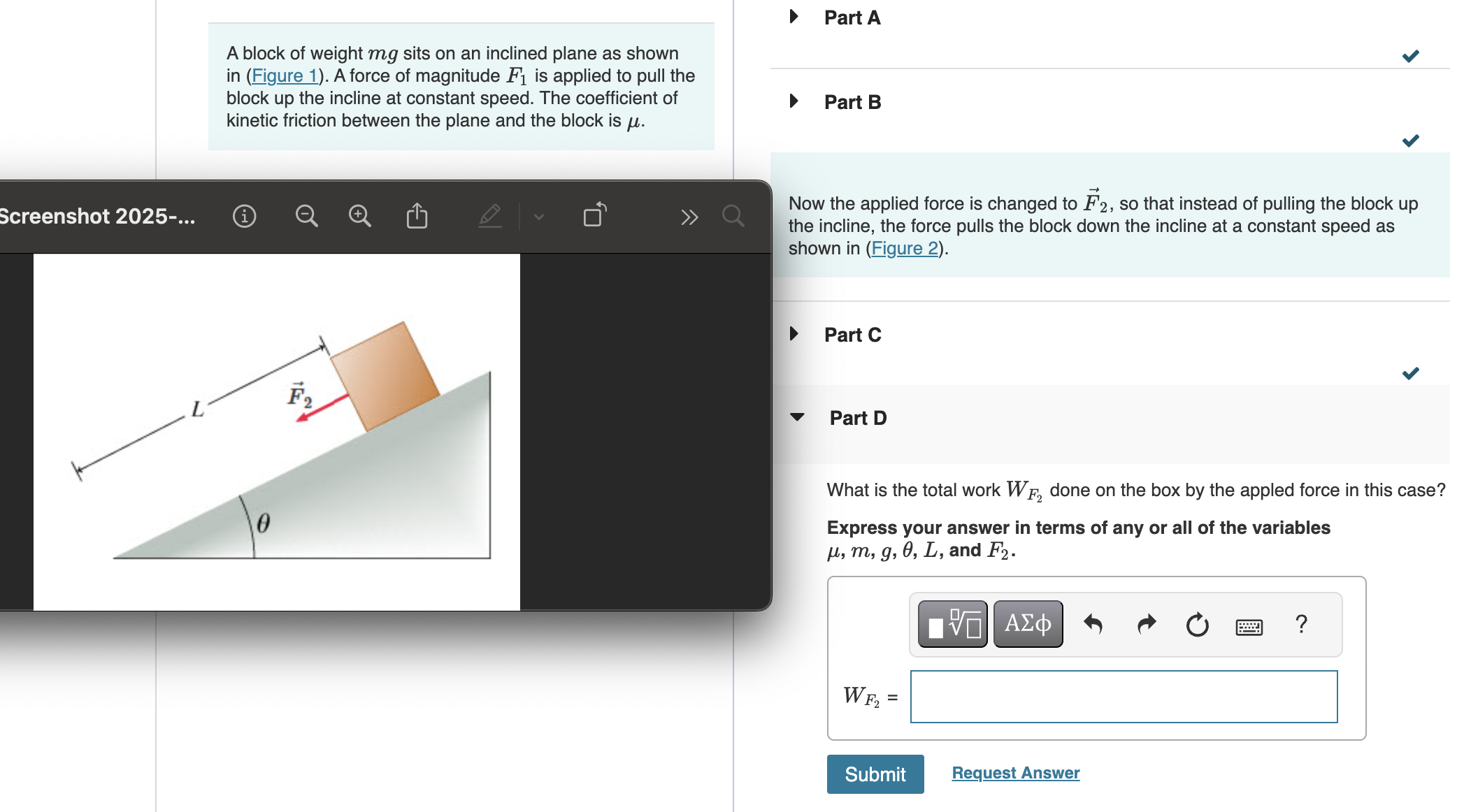
The question is asking for the total work done on a block by a force acting on it while it's on an inclined plane. The user is required to express this work in terms of various given variables like mass, gravitational force, angle, length, and the force applied.
Answer
$$ W_{F_2} = mgL(\sin(\theta) + \mu \cos(\theta)) $$
Answer for screen readers
$$ W_{F_2} = mgL(\sin(\theta) + \mu \cos(\theta)) $$
Steps to Solve
- Identify the forces acting on the block
The forces acting on the block on the inclined plane are:
- Weight of the block: $W = mg$, acting vertically downward.
- Normal force $N$, acting perpendicular to the plane.
- Frictional force $f_k$, acting opposite to the direction of motion.
- Applied force $F_2$, pulling the block down the incline.
- Calculate the frictional force
The frictional force is given by the equation: $$ f_k = \mu N $$
Where $N$ is the normal force. The normal force on an incline can be calculated as: $$ N = mg \cos(\theta) $$
Therefore, the kinetic friction force becomes: $$ f_k = \mu mg \cos(\theta) $$
- Set up the net forces along the plane
Since the block is moving at a constant speed, the net force is zero: $$ F_2 - mg \sin(\theta) - f_k = 0 $$
Substituting for $f_k$, we have: $$ F_2 - mg \sin(\theta) - \mu mg \cos(\theta) = 0 $$
Rearranging gives: $$ F_2 = mg \sin(\theta) + \mu mg \cos(\theta) $$
- Express the work done by the force (F_2)
Work done by the force (F_2) while moving a distance (L) down the incline is given by: $$ W_{F_2} = F_2 \cdot L $$
Substituting for (F_2), we get: $$ W_{F_2} = (mg \sin(\theta) + \mu mg \cos(\theta)) \cdot L $$
- Final expression for the work done
Therefore, the total work done on the box by the applied force (F_2) is: $$ W_{F_2} = mgL(\sin(\theta) + \mu \cos(\theta)) $$
$$ W_{F_2} = mgL(\sin(\theta) + \mu \cos(\theta)) $$
More Information
The work done by the applied force (F_2) considers both the gravitational component acting along the incline and the frictional force opposing the motion. It's essential to account for both when determining the net force and the work.
Tips
One common mistake is neglecting the frictional force when calculating (F_2) or omitting the angle dependence in the trigonometric functions. Always ensure that all forces acting along and perpendicular to the incline are considered to calculate the normal force and friction correctly.
AI-generated content may contain errors. Please verify critical information