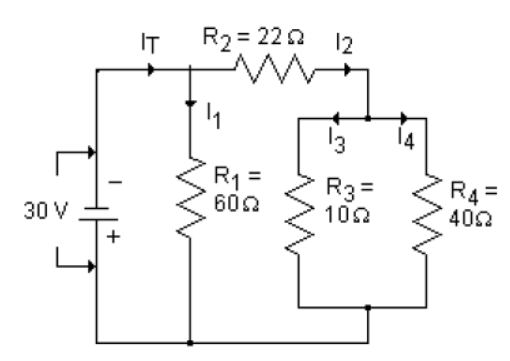
What is the total resistance in the circuit?
Understand the Problem
The question asks for the total resistance in a given electrical circuit with multiple resistors. To find the total resistance, we need to analyze the circuit configuration (series or parallel) and apply the appropriate formulas.
Answer
The total resistance is $R_T = 68 \, \Omega$.
Answer for screen readers
The total resistance in the circuit is $R_T = 68 , \Omega$.
Steps to Solve
- Identify the Resistor Configuration
In the given circuit, $R_1$ is in series with a parallel combination of $R_3$ and $R_4$. The first step is to recognize that $R_1$ and the parallel network form two different paths for current.
- Calculate the Equivalent Resistance of R3 and R4 in Parallel
To find the equivalent resistance ($R_{eq}$) of $R_3$ and $R_4$ in parallel, use the formula:
$$ \frac{1}{R_{eq}} = \frac{1}{R_3} + \frac{1}{R_4} $$
Substituting the values:
$$ \frac{1}{R_{eq}} = \frac{1}{10} + \frac{1}{40} $$
- Calculate R_eq
To simplify and calculate $R_{eq}$, first find a common denominator:
$$ \frac{1}{R_{eq}} = \frac{4 + 1}{40} = \frac{5}{40} $$
Thus,
$$ R_{eq} = \frac{40}{5} = 8 , \Omega $$
- Combine R1 and R_eq in Series
Now add $R_1$ and $R_{eq}$ together to find the total resistance ($R_T$):
$$ R_T = R_1 + R_{eq} $$
Substituting the values:
$$ R_T = 60 + 8 = 68 , \Omega $$
The total resistance in the circuit is $R_T = 68 , \Omega$.
More Information
The total resistance is crucial in understanding how much current will flow through the circuit for a given voltage. The overall behavior of the circuit, including current distribution, depends significantly on these resistor configurations.
Tips
- A common mistake is miscalculating the equivalent resistance of resistors in parallel. Always ensure to use the correct formula and double-check calculations, especially common denominators.
- Confusing series and parallel calculations—remember, in series, resistances add directly, while in parallel, you use reciprocal formulas.
