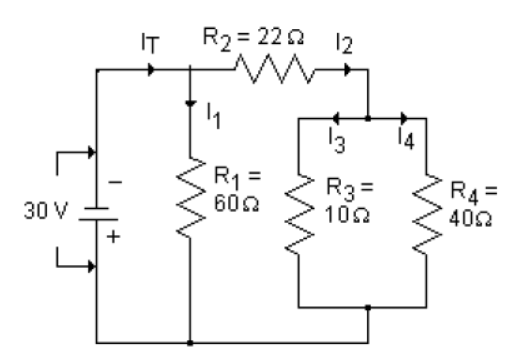
What is the total current in the circuit?

Steps to Solve

1. Calculate the equivalent resistance of resistors R3 and R4 in parallel

The resistors R3 and R4 are in parallel. The formula for equivalent resistance ($R_{eq}$) of parallel resistors is:

$$ \frac{1}{R_{eq}} = \frac{1}{R_3} + \frac{1}{R_4} $$

Substituting the values, we get:

$$ \frac{1}{R_{eq}} = \frac{1}{10 , \Omega} + \frac{1}{40 , \Omega} $$

Calculating:

$$ \frac{1}{R_{eq}} = \frac{4}{40} + \frac{1}{40} = \frac{5}{40} = \frac{1}{8} $$

Thus,

$$ R_{eq} = 8 , \Omega $$

2. Compute the total resistance of the circuit

The total resistance ($R_T$) in the circuit can now be found by adding the resistance of R1 (in series) with the equivalent resistance of R3 and R4 (calculated previously):

$$ R_T = R_1 + R_{eq} $$

Substituting the values:

$$ R_T = 60 , \Omega + 8 , \Omega = 68 , \Omega $$

3. Apply Ohm's Law to find the total current

Now we can use Ohm's law, which states $V = I \cdot R$, to find the total current ($I_T$):

$$ I_T = \frac{V}{R_T} $$

Substituting the values:

$$ I_T = \frac{30 , V}{68 , \Omega} \approx 0.441 , A $$