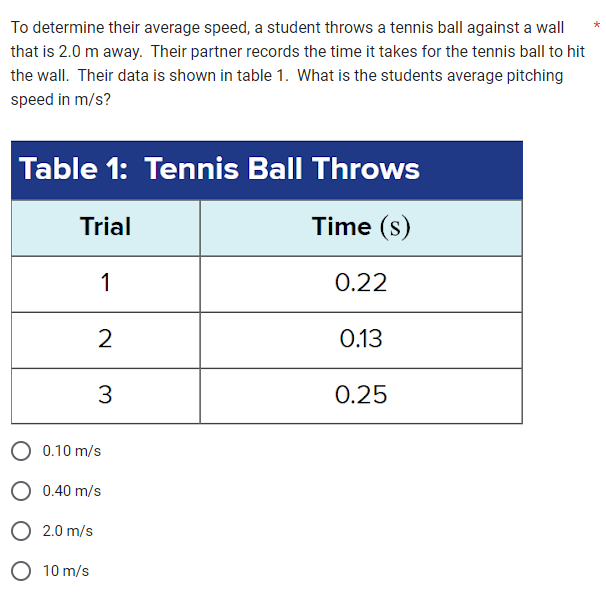
What is the student's average pitching speed in m/s?
Understand the Problem
The question is asking for the average speed of a tennis ball thrown towards a wall that is 2.0 meters away, based on the recorded times from three trials. To solve this, we will calculate the average speed using the formula speed = distance/time for each trial and then take the average of those speeds.
Answer
The average pitching speed is approximately $10.82 \text{ m/s}$.
Answer for screen readers
The average pitching speed is approximately $10.82 \text{ m/s}$.
Steps to Solve
- Identify the distance and times The distance to the wall is 2.0 meters. The recorded times for each trial are:
- Trial 1: 0.22 s
- Trial 2: 0.13 s
- Trial 3: 0.25 s
- Calculate the speed for each trial Use the formula for speed: $$ \text{speed} = \frac{\text{distance}}{\text{time}} $$
For Trial 1: $$ \text{speed}_1 = \frac{2.0 \text{ m}}{0.22 \text{ s}} \approx 9.09 \text{ m/s} $$
For Trial 2: $$ \text{speed}_2 = \frac{2.0 \text{ m}}{0.13 \text{ s}} \approx 15.38 \text{ m/s} $$
For Trial 3: $$ \text{speed}_3 = \frac{2.0 \text{ m}}{0.25 \text{ s}} = 8.00 \text{ m/s} $$
- Calculate the average speed Now, we calculate the average speed using the speeds from all trials: $$ \text{average speed} = \frac{\text{speed}_1 + \text{speed}_2 + \text{speed}_3}{3} $$
Substituting the values: $$ \text{average speed} = \frac{9.09 \text{ m/s} + 15.38 \text{ m/s} + 8.00 \text{ m/s}}{3} $$
- Perform the addition and division Calculating the total speed: $$ 9.09 + 15.38 + 8.00 = 32.47 $$
Now divide by 3: $$ \text{average speed} = \frac{32.47 \text{ m/s}}{3} \approx 10.82 \text{ m/s} $$
The average pitching speed is approximately $10.82 \text{ m/s}$.
More Information
The speed was calculated by averaging the speeds obtained from the distances and times across multiple trials. This process accounts for any inconsistencies in throw strength or technique.
Tips
- Forgetting to convert time to seconds if it is provided in milliseconds.
- Not using the correct formula for speed ($\text{speed} = \frac{\text{distance}}{\text{time}}$).
- Failing to average the speeds correctly by not summing all speeds first.
AI-generated content may contain errors. Please verify critical information