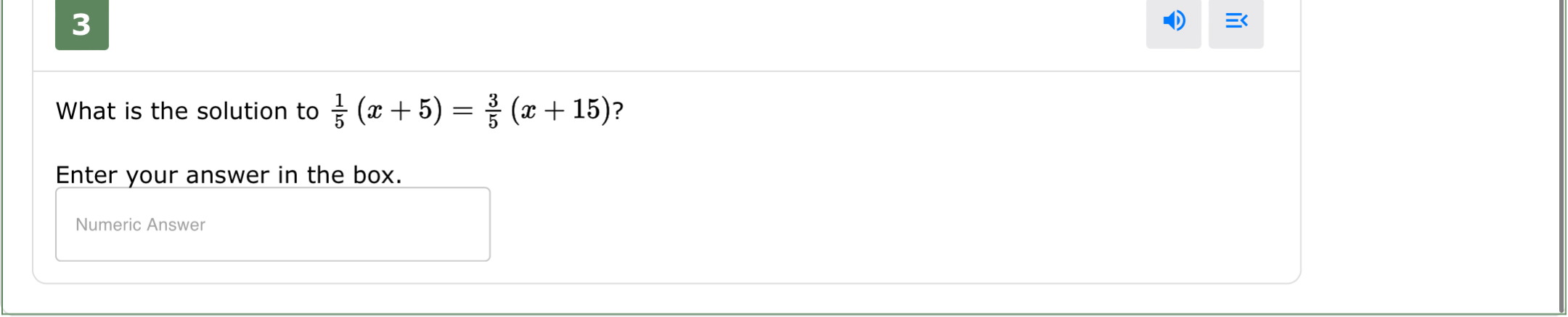
What is the solution to \( \frac{1}{5} (x + 5) = \frac{3}{5} (x + 15) \)?
Understand the Problem
The question is asking for the solution to the equation where one side is a fraction multiplied by a binomial expression and the other side is another fraction multiplied by a different binomial expression. To solve this, we will set up the equation and isolate the variable x.
Answer
The solution is \( x = -20 \).
Answer for screen readers
The solution is ( x = -20 ).
Steps to Solve
- Clear the fractions
To eliminate the fractions, multiply both sides of the equation by 5:
$$ 5 \cdot \frac{1}{5}(x + 5) = 5 \cdot \frac{3}{5}(x + 15) $$
This simplifies to:
$$ x + 5 = 3(x + 15) $$
- Distribute on the right side
Distribute the 3 on the right side of the equation:
$$ x + 5 = 3x + 45 $$
- Rearrange the equation
To isolate $x$, first, subtract $x$ from both sides:
$$ 5 = 3x - x + 45 $$
This simplifies to:
$$ 5 = 2x + 45 $$
- Isolate $x$
Next, subtract 45 from both sides:
$$ 5 - 45 = 2x $$
Thus,
$$ -40 = 2x $$
- Solve for $x$
Finally, divide by 2:
$$ x = \frac{-40}{2} = -20 $$
The solution is ( x = -20 ).
More Information
This equation demonstrates the principles of distributing and simplifying equations. It's a typical example of solving linear equations involving fractions.
Tips
- Forgetting to distribute correctly may lead to incorrect terms.
- Neglecting to combine like terms properly can also lead to mistakes in isolating the variable.
- Trying to eliminate fractions without multiplying both sides by the same number.
AI-generated content may contain errors. Please verify critical information