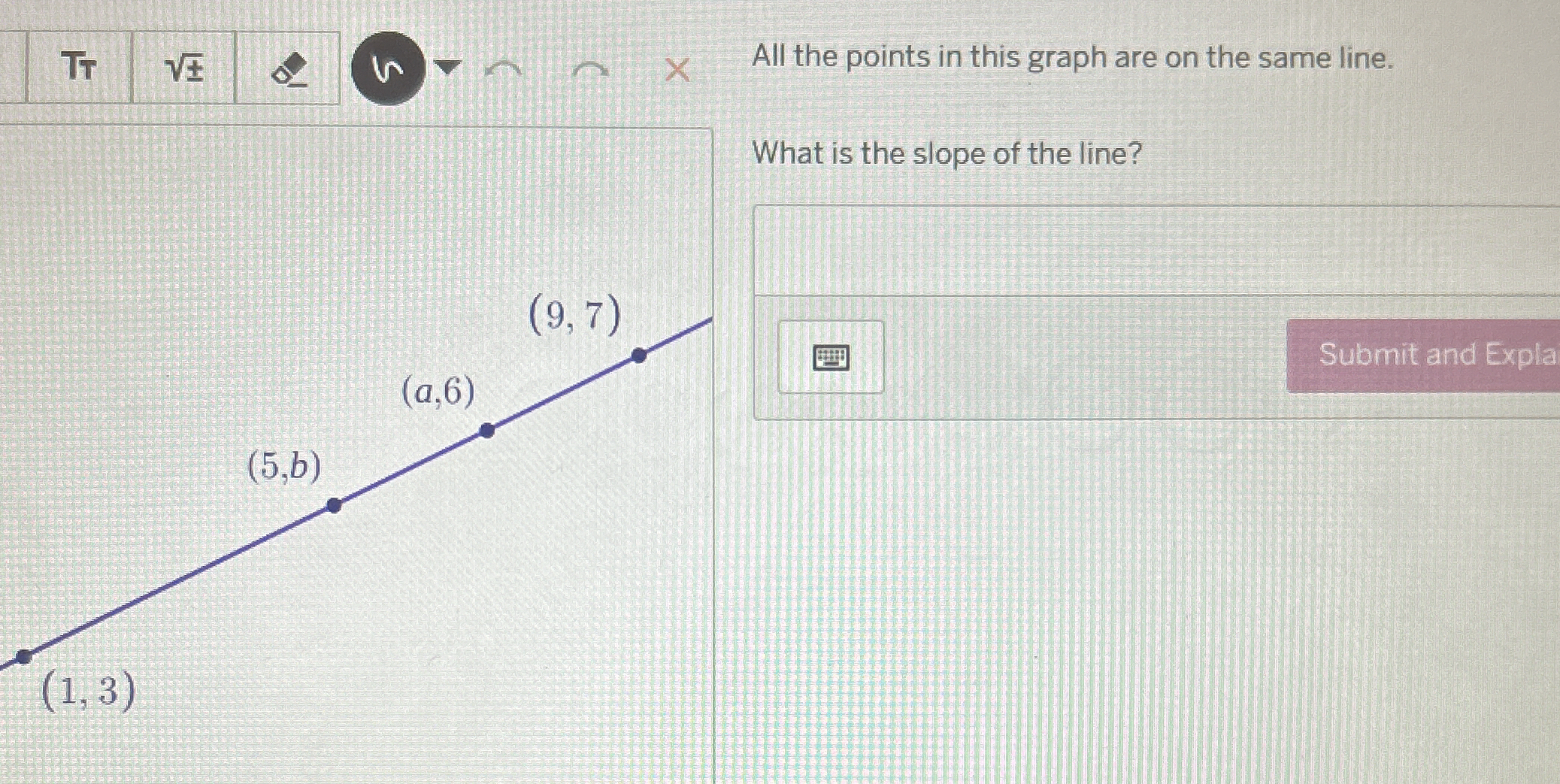
What is the slope of the line?
Understand the Problem
The question is asking for the slope of a line that passes through a given set of points (1, 3), (5, b), (a, 6), and (9, 7). To find the slope, we can use the slope formula, which involves the coordinates of two points on the line.
Answer
The slope of the line is \( \frac{1}{2} \).
Answer for screen readers
The slope of the line is ( \frac{1}{2} ).
Steps to Solve
-
Identify Points for Calculation
We'll use two known points on the line: ( (1, 3) ) and ( (9, 7) ) to calculate the slope. -
Use the Slope Formula
The slope ( m ) of a line between two points ( (x_1, y_1) ) and ( (x_2, y_2) ) is given by:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ -
Substitute Values from the Points
Using the points ( (1, 3) ) and ( (9, 7) ):
- ( x_1 = 1 ), ( y_1 = 3 )
- ( x_2 = 9 ), ( y_2 = 7 )
Substituting these values into the slope formula:
$$ m = \frac{7 - 3}{9 - 1} $$
-
Calculate the Slope
Now, we compute the values:
$$ m = \frac{4}{8} = \frac{1}{2} $$ -
Conclusion
The slope of the line that passes through all the points is ( \frac{1}{2} ).
The slope of the line is ( \frac{1}{2} ).
More Information
The slope indicates how steep the line is. A slope of ( \frac{1}{2} ) means that for every 2 units you move horizontally, the line rises 1 unit vertically.
Tips
- Forgetting to use the correct order in the slope formula: Always ensure the ( y ) and ( x ) values in the formula correspond correctly to the points used.
- Calculating the change in ( y ) or ( x ) incorrectly: Double-check arithmetic calculations.
AI-generated content may contain errors. Please verify critical information