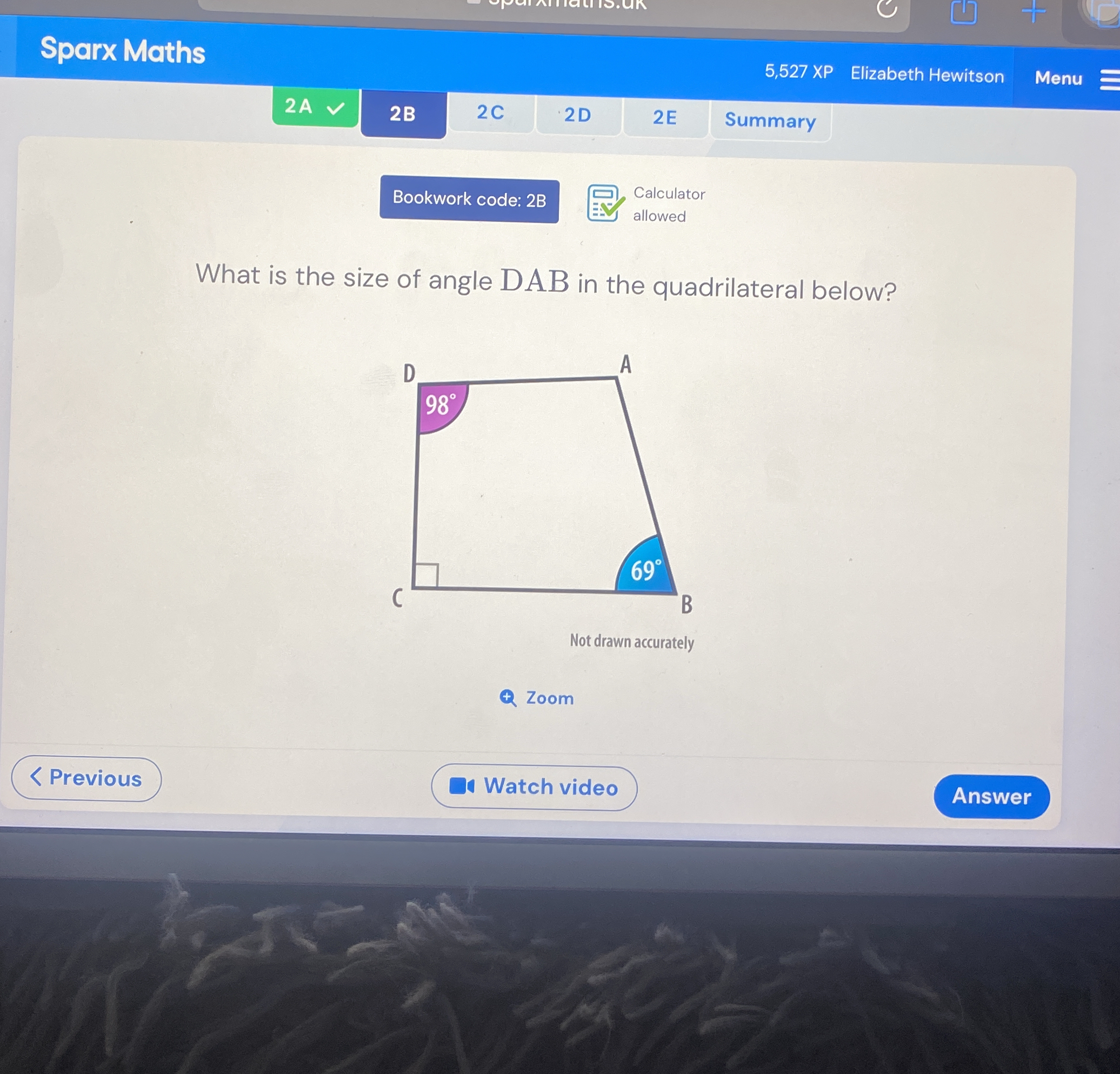
What is the size of angle DAB in the quadrilateral below?
Understand the Problem
The question is asking for the measurement of angle DAB in the given quadrilateral, where the measures of other angles are provided. To solve this, we will apply the properties of a quadrilateral, specifically that the sum of angles in a quadrilateral is 360 degrees.
Answer
The measure of angle DAB is $103^\circ$.
Answer for screen readers
The measure of angle DAB is $103^\circ$.
Steps to Solve
-
Identify the known angles The known angles in the quadrilateral are $\angle DAB = x$, $\angle ABC = 69^\circ$, and $\angle ADC = 98^\circ$.
-
Apply the angle sum property of a quadrilateral The sum of the interior angles of a quadrilateral is $360^\circ$. Therefore, we can write the equation as:
$$ x + 69^\circ + 98^\circ + \angle BCD = 360^\circ $$
-
Find angle BCD Since angle BCD is a right angle, we can state that $\angle BCD = 90^\circ$.
-
Substitute values into the equation Now we can substitute the known angles into the equation:
$$ x + 69^\circ + 98^\circ + 90^\circ = 360^\circ $$
- Combine like terms Add together the known angle measures:
$$ x + 69^\circ + 98^\circ + 90^\circ = x + 257^\circ $$
- Solve for angle DAB (x) Now we can set up the equation:
$$ x + 257^\circ = 360^\circ $$
Subtract $257^\circ$ from both sides:
$$ x = 360^\circ - 257^\circ $$
- Calculate the value of x Now, perform the subtraction:
$$ x = 103^\circ $$
The measure of angle DAB is $103^\circ$.
More Information
In any quadrilateral, the sum of internal angles always totals to $360^\circ$. Recognizing this property allows us to find unknown angles when some angles are already given. Here, knowing that one angle is $90^\circ$ simplifies the calculation.
Tips
- Forgetting that the sum of angles in a quadrilateral is $360^\circ$.
- Confusing angle types—always ensure you're clear about right angles.
AI-generated content may contain errors. Please verify critical information