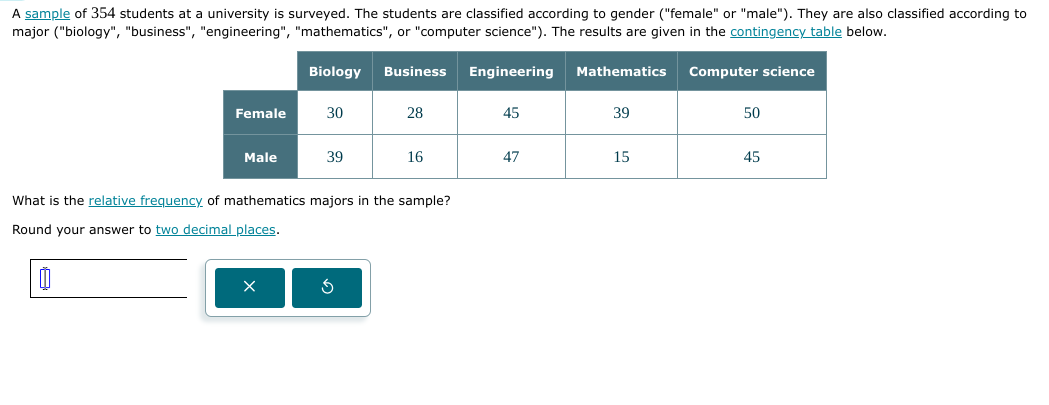
What is the relative frequency of mathematics majors in the sample? Round your answer to two decimal places.
Understand the Problem
The question is asking to calculate the relative frequency of students majoring in mathematics from a survey of 354 students. This involves finding the total number of mathematics majors and dividing it by the total number of students, then rounding the answer to two decimal places.
Answer
$0.15$
Answer for screen readers
The relative frequency of mathematics majors in the sample is approximately $0.15$.
Steps to Solve
- Identify the number of mathematics majors
From the table, we need to find the number of students majoring in mathematics. We will sum the values from the mathematics column for both genders.
[ \text{Mathematics Majors} = 39 \text{ (female)} + 15 \text{ (male)} = 54 ]
- Calculate the relative frequency
The relative frequency of mathematics majors is calculated by dividing the number of mathematics majors by the total number of surveyed students.
[ \text{Relative Frequency} = \frac{\text{Mathematics Majors}}{\text{Total Students}} = \frac{54}{354} ]
- Perform the division
Now calculate the division to find the relative frequency.
[ \text{Relative Frequency} \approx 0.15254 ]
- Round to two decimal places
Finally, we round the calculated relative frequency to two decimal places.
[ \text{Relative Frequency (rounded)} \approx 0.15 ]
The relative frequency of mathematics majors in the sample is approximately $0.15$.
More Information
This relative frequency indicates that about 15% of the surveyed students are majoring in mathematics. Relative frequency helps to understand the proportion of a subgroup within a larger group and is often used in statistics.
Tips
- Forgetting to add up the majors for both genders.
- Not rounding the final answer to the specified number of decimal places.
- Miscalculating the total number of students, leading to incorrect relative frequency.
AI-generated content may contain errors. Please verify critical information