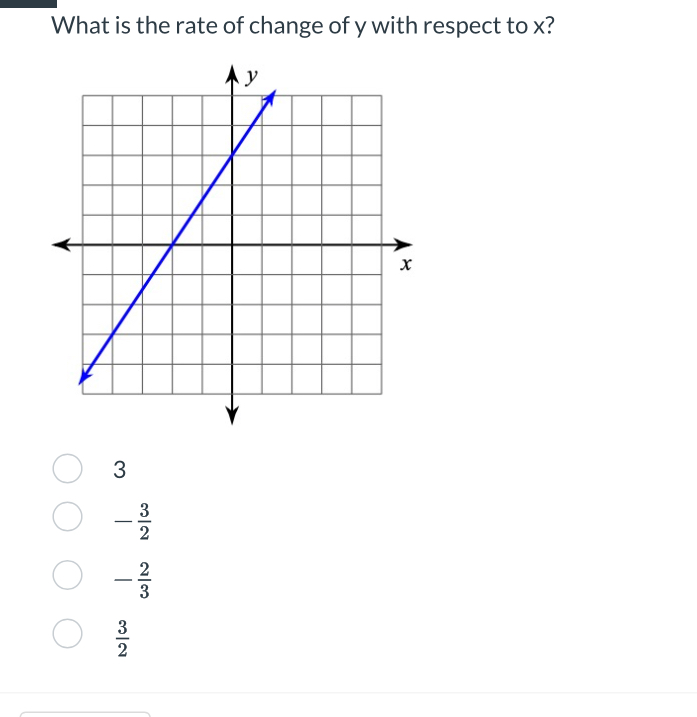
What is the rate of change of y with respect to x?
Understand the Problem
The question is asking for the rate of change of y with respect to x based on the provided linear graph. This involves determining the slope of the line depicted in the graph.
Answer
The rate of change is $\frac{1}{3}$.
Answer for screen readers
The rate of change of $y$ with respect to $x$ is $\frac{1}{3}$.
Steps to Solve
- Identify Two Points on the Line
To determine the rate of change (slope), select two points on the line. From the graph, let’s choose the points (1, 2) and (4, 3).
- Calculate the Change in y (Δy)
Using the formula for change in y: $$ \Delta y = y_2 - y_1 $$ Substituting in our points $(x_1, y_1) = (1, 2)$ and $(x_2, y_2) = (4, 3)$: $$ \Delta y = 3 - 2 = 1 $$
- Calculate the Change in x (Δx)
Using the formula for change in x: $$ \Delta x = x_2 - x_1 $$ Substituting in our values: $$ \Delta x = 4 - 1 = 3 $$
- Determine the Slope (Rate of Change)
Now, use the formula for slope (rate of change): $$ \text{slope} = \frac{\Delta y}{\Delta x} = \frac{1}{3} $$
The rate of change of $y$ with respect to $x$ is $\frac{1}{3}$.
More Information
The slope of a line represents the rate of change of the dependent variable (y) with respect to the independent variable (x). A slope of $\frac{1}{3}$ means that for every 1 unit increase in $y$, $x$ increases by 3 units.
Tips
- Choosing Incorrect Points: Ensure the selected points are exactly on the line.
- Forgetting Slope Formula: Remember to use the correct formula for the slope, which is the rise over run.
AI-generated content may contain errors. Please verify critical information