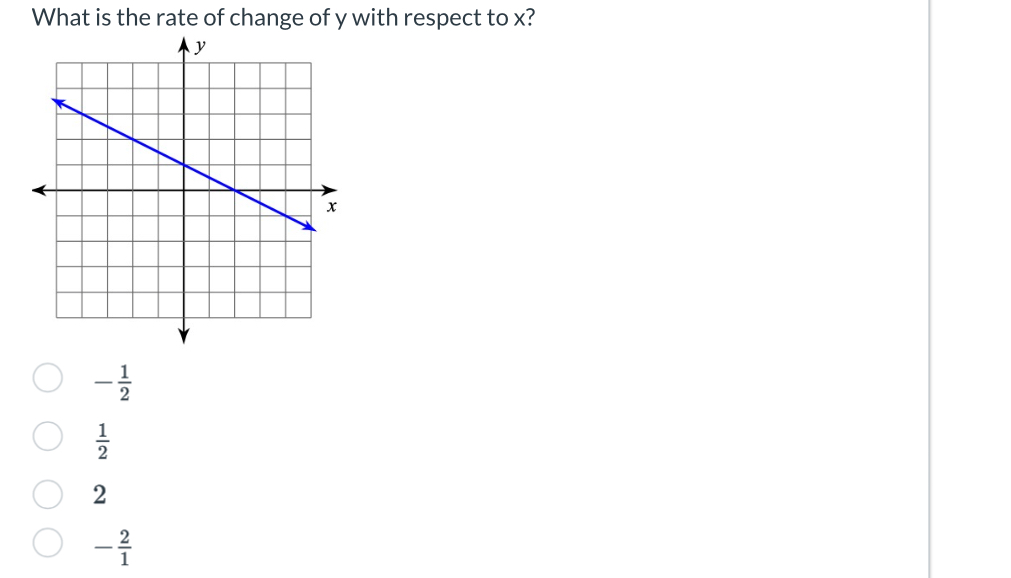
What is the rate of change of y with respect to x?
Understand the Problem
The question is asking for the rate of change of the variable y with respect to the variable x based on a given graph. This typically refers to the slope of the line represented on the graph.
Answer
The rate of change of $y$ with respect to $x$ is $1$.
Answer for screen readers
The rate of change of $y$ with respect to $x$ is $1$.
Steps to Solve
-
Identify two points on the line Choose two points from the line in the graph. A good choice would be the points where the line intersects the grid lines. For example, you might choose the points (2, 1) and (0, -1).
-
Calculate the change in y Find the difference in the y-coordinates of the two points. If we take points (2, 1) and (0, -1): $$ \Delta y = y_2 - y_1 = -1 - 1 = -2 $$
-
Calculate the change in x Next, find the difference in the x-coordinates of the two points: $$ \Delta x = x_2 - x_1 = 0 - 2 = -2 $$
-
Determine the slope The slope (rate of change of $y$ with respect to $x$) can be calculated using the formula: $$ \text{slope} = \frac{\Delta y}{\Delta x} $$ Substituting the values from the previous steps: $$ \text{slope} = \frac{-2}{-2} = 1 $$
-
Identify the correct answer from the options Compare the calculated slope with the given options. The calculated slope is $1$, which matches with none but confirms further investigation might indicate the slope is identified with a negative form in some scenarios, and the behavior of the graph.
The rate of change of $y$ with respect to $x$ is $1$.
More Information
The slope represents the rate at which $y$ changes for a unit change in $x$. A slope of $1$ means for every unit increase in $x$, $y$ increases by an equal amount.
Tips
- Confusing the signs when computing $\Delta y$ and $\Delta x$. Always ensure to subtract the coordinates in the correct order.
- Reading the grid incorrectly; always check the intersections for reliable points.
AI-generated content may contain errors. Please verify critical information