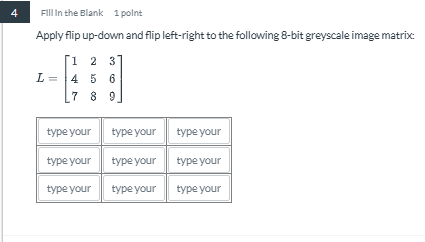
Apply flip up-down and flip left-right to the following 8-bit grayscale image matrix: L = [1 2 3; 4 5 6; 7 8 9]
Understand the Problem
The question is asking to apply two transformations (flip up-down and flip left-right) to a specified 8-bit grayscale image matrix. The user needs to provide the resulting matrix after these transformations.
Answer
$$ L_{final} = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix} $$
Answer for screen readers
The resulting matrix after applying both transformations is:
$$ L_{final} = \begin{bmatrix} 9 & 8 & 7 \ 6 & 5 & 4 \ 3 & 2 & 1 \end{bmatrix} $$
Steps to Solve
- Flip Up-Down Transformation
To flip the matrix up-down, we reverse the order of the rows. The original matrix is:
$$ L = \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{bmatrix} $$
After flipping up-down, the matrix becomes:
$$ L_{up-down} = \begin{bmatrix} 7 & 8 & 9 \ 4 & 5 & 6 \ 1 & 2 & 3 \end{bmatrix} $$
- Flip Left-Right Transformation
Next, we flip the resulting matrix left-right, which involves reversing the elements in each row. Starting from the matrix obtained after the up-down flip:
$$ L_{up-down} = \begin{bmatrix} 7 & 8 & 9 \ 4 & 5 & 6 \ 1 & 2 & 3 \end{bmatrix} $$
After flipping left-right, the matrix becomes:
$$ L_{final} = \begin{bmatrix} 9 & 8 & 7 \ 6 & 5 & 4 \ 3 & 2 & 1 \end{bmatrix} $$
The resulting matrix after applying both transformations is:
$$ L_{final} = \begin{bmatrix} 9 & 8 & 7 \ 6 & 5 & 4 \ 3 & 2 & 1 \end{bmatrix} $$
More Information
The transformations applied to the matrix effectively reverse the order of the rows and the order of the elements within each row. This is a common operation in image processing to enhance visual representation or achieve specific layouts.
Tips
- Forgetting the Order of Transformations: Sometimes, it's easy to confuse which transformation to perform first. Always remember to apply the transformations in the given order.
- Misunderstanding Flips: Flipping left-right means reversing elements within each row, while flipping up-down means reversing the row order.
AI-generated content may contain errors. Please verify critical information