What is the output voltage (Vout) of the given op-amp circuit?
Understand the Problem
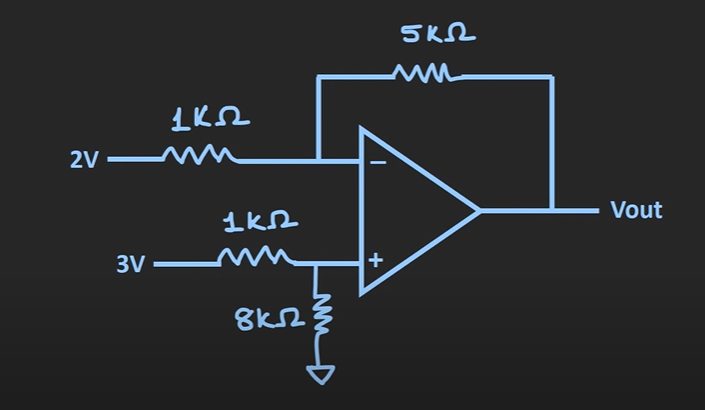
The question involves analyzing an operational amplifier (op-amp) circuit to find the output voltage (Vout) based on the given input voltages and resistor values.
Answer
The output voltage is approximately $4.06V$.
Answer for screen readers
The output voltage $V_{out}$ is approximately $4.06V$.
Steps to Solve
- Identifying the Circuit Configuration
The circuit consists of a non-inverting op-amp configuration. The non-inverting input is connected to a voltage divider formed by two resistors.
- Calculating the Non-Inverting Input Voltage ($V_+$)
To find the non-inverting input voltage $V_+$, use the voltage divider formula:
$$ V_+ = \frac{R_2}{R_1 + R_2} \times V_{in} $$
Here, resistor values are:
- $R_1 = 1 , kΩ$ (between 2V and $V_+$)
- $R_2 = 1 , kΩ$ (between 3V and $V_+$)
- $V_{in} = 2V$ (top voltage)
Calculate $V_+$ by considering the voltage at the non-inverting input:
$$ V_+ = \frac{1kΩ}{1kΩ + 1kΩ} \times (2V - 3V) + 3V = \frac{1}{2}(-1) + 3 = 2.5V $$
- Calculating the Inverting Input Voltage ($V_-$)
Use the voltage divider again for the inverting input voltage $V_-$. The input voltage is the output voltage $V_{out}$ and we consider the feedback from the output through the $5kΩ$ resistor:
$$ V_- = \frac{V_{out}}{5kΩ + 8kΩ} \cdot 8kΩ $$
- Setting Up the Feedback Loop
In a proper op-amp operation (assuming ideal), $V_+ \approx V_-$. Therefore, set the two equations equal to each other:
$$ 2.5V = \frac{V_{out}}{5kΩ + 8kΩ} \cdot 8kΩ $$
Solve for $V_{out}$:
$$ V_{out} = 2.5V \cdot \frac{5kΩ + 8kΩ}{8kΩ} $$
- Calculating the Final Output Voltage ($V_{out}$)
Substituting, we have:
$$ V_{out} = 2.5V \cdot \frac{13kΩ}{8kΩ} $$
- Final Calculation
Now perform the final multiplication:
$$ V_{out} = 2.5V \cdot 1.625 = 4.0625V $$
The output voltage $V_{out}$ is approximately $4.06V$.
More Information
In op-amp circuits, the output voltage is largely determined by the input voltages and the feedback resistances. The voltage divider effect significantly influences how these voltages interact at the op-amp inputs, demonstrating the importance of understanding resistor networks in circuit analysis.
Tips
- Incorrectly applying the voltage divider: Always ensure that the correct resistors are used in the voltage divider formula.
- Neglecting feedback resistances: The effect of feedback resistances on $V_-$ compared to $V_+$ is often overlooked, which can throw off calculations.
AI-generated content may contain errors. Please verify critical information