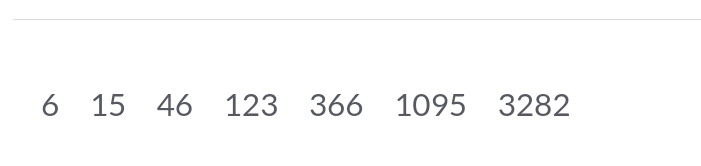
What is the next number in the sequence: 6, 15, 46, 123, 366, 1095, 3282?

Steps to Solve

1. Identify the differences between numbers

First, calculate the differences between consecutive numbers to find a pattern:

• $15 - 6 = 9$
• $46 - 15 = 31$
• $123 - 46 = 77$
• $366 - 123 = 243$
• $1095 - 366 = 729$
• $3282 - 1095 = 2187$

So, the differences are: 9, 31, 77, 243, 729, 2187.

2. Calculate the ratios of the differences

Next, we'll compare these differences to find any relation:

• $31 / 9 \approx 3.44$
• $77 / 31 \approx 2.48$
• $243 / 77 \approx 3.15$
• $729 / 243 = 3$
• $2187 / 729 = 3$

The ratios appear to stabilize around 3 for the larger differences.

3. Notice a pattern in the differences

It seems the differences can follow a pattern of powers of 3. They relate to $3^2 = 9$, $3^3 = 27$, $3^4 = 81$, $3^5 = 243$, and $3^6 = 729$.

4. Predict the next difference

The next difference would likely follow this pattern, which implies the next term could relate to:

$$ 3^7 = 2187 $$

Following the previous difference of $3282$, we add this value:

$$ 3282 + 6561 = 9843 $$

5. Conclusion for the next term

Adding the established pattern gives us the next number in the sequence.