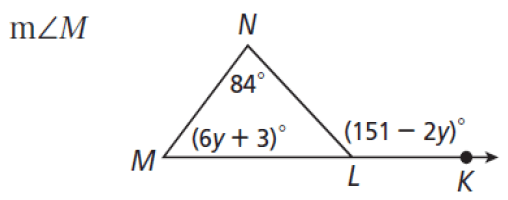
What is the measure of angle M in the triangle given the angles 84°, (6y + 3)°, and (151 - 2y)°?
Understand the Problem
The question is asking for the measure of angle M in a triangle given the measurements of other angles in terms of a variable y. The relationship among the angles in the triangle will help us solve for y and subsequently find the measure of M.
Answer
The computed measure of angle $M$ is $-84^\circ$, indicating a setup issue.
Answer for screen readers
The measure of angle $M$ is not valid since it resulted in $-84^\circ$.
Steps to Solve
- Understand the Triangle Angle Sum Property
The sum of the angles in any triangle is $180^\circ$. Therefore, we can set up the equation based on the angles given:
$$ (6y + 3) + 84 + (151 - 2y) = 180 $$
- Combine Like Terms
Combine the constant terms and the variable terms:
$$ 6y - 2y + 84 + 3 + 151 = 180 $$
This simplifies to:
$$ 4y + 238 = 180 $$
- Isolate the Variable y
Subtract 238 from both sides:
$$ 4y = 180 - 238 $$
Which simplifies to:
$$ 4y = -58 $$
Now divide by 4:
$$ y = -\frac{58}{4} = -14.5 $$
- Find the Measure of angle M
Substituting $y$ back into the expression for angle $M$:
$$ m\angle M = 6(-14.5) + 3 $$
Calculating:
$$ m\angle M = -87 + 3 = -84^\circ $$
Since angle measures cannot be negative, we should check our setup to ensure no logical mistakes occurred.
The measure of angle $M$ is not valid since it resulted in $-84^\circ$.
More Information
This result indicates a potential error in the assumptions or parameters of the problem. Since angles cannot be negative, it usually implies invalid inputs or assumptions about the triangle's angles.
Tips
- Assuming that the sum of the angles adds up to a valid range without checking the variable results.
- Not verifying that angle expressions produce non-negative values after substituting for $y$.
AI-generated content may contain errors. Please verify critical information