What is the initial vertical velocity of the t-shirt (in m/s)?
Understand the Problem
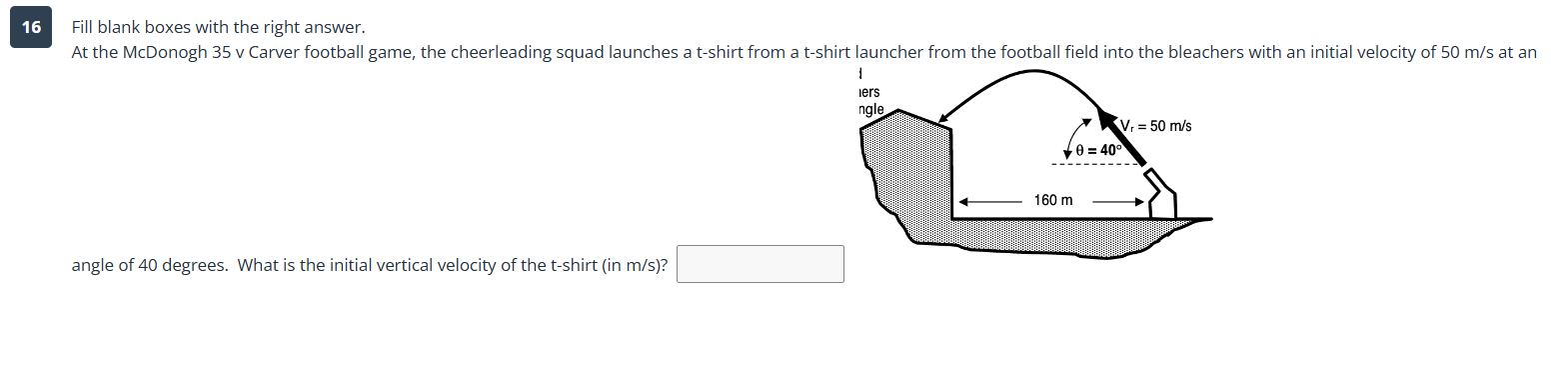
The question is asking for the initial vertical velocity of a t-shirt launched at an angle, using the provided initial velocity of 50 m/s and an angle of 40 degrees. We will use trigonometric functions to determine the vertical component of the initial velocity.
Answer
The initial vertical velocity of the t-shirt is approximately $32.14 \text{ m/s}$.
Answer for screen readers
The initial vertical velocity of the t-shirt is approximately $32.14 \text{ m/s}$.
Steps to Solve
- Identify the components of velocity
To find the initial vertical velocity component ($v_{y}$), we can use the trigonometric sine function since it relates to the angle of launch.
- Use the sine function
The formula for the vertical component of the velocity is:
$$ v_{y} = v \cdot \sin(\theta) $$
Where:
- $v$ is the initial velocity (50 m/s)
- $\theta$ is the angle of launch (40 degrees)
- Substitute the values
Now we substitute the given values into the formula:
$$ v_{y} = 50 \cdot \sin(40^\circ) $$
- Calculate the sine value
First, calculate $\sin(40^\circ)$. This value is approximately $0.6428$.
- Complete the calculation
Now calculate:
$$ v_{y} = 50 \cdot 0.6428 $$
This results in:
$$ v_{y} \approx 32.14 \text{ m/s} $$
The initial vertical velocity of the t-shirt is approximately $32.14 \text{ m/s}$.
More Information
The vertical velocity component helps determine how high the object will rise before falling back down, a key aspect of projectile motion. Understanding this concept is vital for anyone studying physics or engineering.
Tips
- Confusing angle types: Sometimes, students mix up degrees and radians when calculating the sine of an angle. Always ensure your calculator is set to the correct mode.
- Forgetting the sine function: Some might mistakenly try to use cosine instead of sine for vertical components. Remember, the vertical component uses $\sin$.
