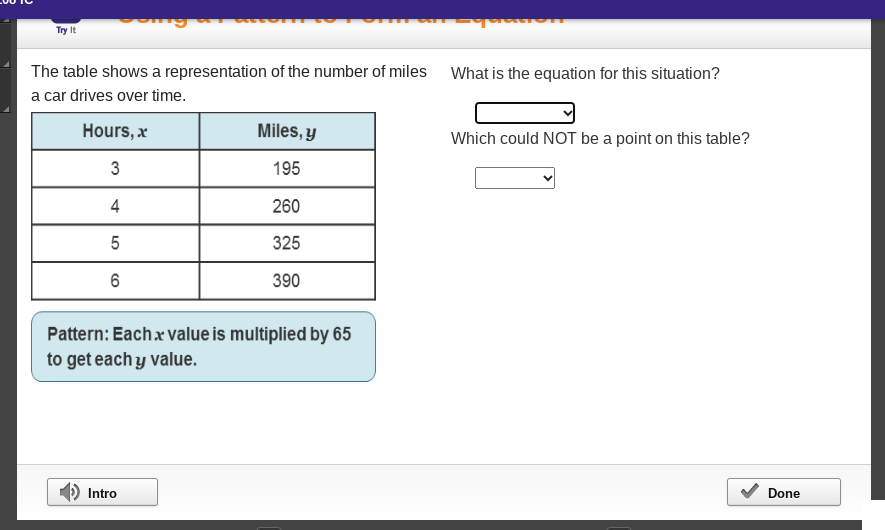
What is the equation for this situation? Which could NOT be a point on this table?
Understand the Problem
The question is asking for the equation that describes the relationship between hours driven (x) and miles driven (y) based on the table provided. It also seeks to identify a point that could not be represented in the table’s data. The key concepts include forming a linear equation from a proportional relationship and recognizing valid data points.
Answer
The equation is $$ y = 65x $$.
Answer for screen readers
The equation for this situation is $$ y = 65x $$.
Steps to Solve
-
Identifying the Relationship Between Variables
The table shows a pattern where each hour driven (x) corresponds to a specific number of miles driven (y). The relationship given is that for each hour, the miles are calculated by multiplying the hours by 65. -
Formulating the Equation
To form the equation based on the relationship identified, we can express it as:
$$ y = 65x $$
This means for every hour driven (x), the miles driven (y) is calculated by multiplying the number of hours by 65. -
Verifying the Points in the Table
Check each entry in the table using the equation ( y = 65x ):- For ( x = 3 ):
$$ y = 65 \times 3 = 195 $$ - For ( x = 4 ):
$$ y = 65 \times 4 = 260 $$ - For ( x = 5 ):
$$ y = 65 \times 5 = 325 $$ - For ( x = 6 ):
$$ y = 65 \times 6 = 390 $$
All points in the table match the equation.
- For ( x = 3 ):
-
Finding Points Not in the Table
To identify a point that could NOT be represented in the table, we need to determine values of ( x ) that don't yield integer results for ( y ) or don't fit the pattern. For example, if ( x = 7 ):
$$ y = 65 \times 7 = 455 $$
If this point (7, 455) was not included, then it could NOT be a point in the table.
The equation for this situation is $$ y = 65x $$.
More Information
This equation represents a direct proportional relationship between the hours driven and miles driven. Each hour corresponds to a fixed number of miles driven, making it linear.
Tips
- Not recognizing the pattern of multiplication when forming the equation.
- Miscalculating the values of $y$ for given $x$ values.
- Overlooking potential values for $x$ that don't correspond to the data in the table.
