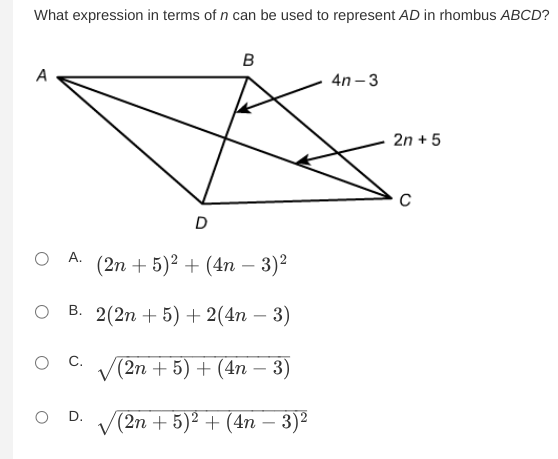
What expression in terms of n can be used to represent AD in rhombus ABCD?

Steps to Solve

1. Identify the Properties of the Rhombus

In a rhombus, all four sides are of equal length. We also know that the diagonals bisect each other at right angles. Therefore, we can use the lengths of the segments formed by the diagonals to find the length of side AD.

2. Set up the expression for the length of the diagonal

From the diagram, we have the segments along the diagonals:

• For diagonal AC, we have two segments: $2n + 5$ and $4n - 3$.

Since the diagonals bisect each other, we can find the lengths of the two triangles formed by the diagonals:

• The lengths are $AD$ and are equal to the length of half the diagonals, so we need to relate this back to the segments.

3. Use the Pythagorean theorem

To find the length of side $AD$, we will use the Pythagorean theorem. In triangle $ABD$, we have:

$$ AD^2 = \left(\frac{(2n + 5)}{2}\right)^2 + \left(\frac{(4n - 3)}{2}\right)^2 $$

This gives us:

$$ AD^2 = \frac{(2n + 5)^2}{4} + \frac{(4n - 3)^2}{4} $$

Combining the fractions, we get:

$$ AD^2 = \frac{(2n + 5)^2 + (4n - 3)^2}{4} $$

Taking the square root, we find:

$$ AD = \sqrt{\frac{(2n + 5)^2 + (4n - 3)^2}{4}} $$

This simplifies to:

$$ AD = \frac{\sqrt{(2n + 5)^2 + (4n - 3)^2}}{2} $$

4. identify the possible expressions

Now we can check our findings against the answer choices provided in the question.