- 3r^3w^4(2r^2w)^2(-3r^2)(4rw^2)^3(2r^2w^3)^4
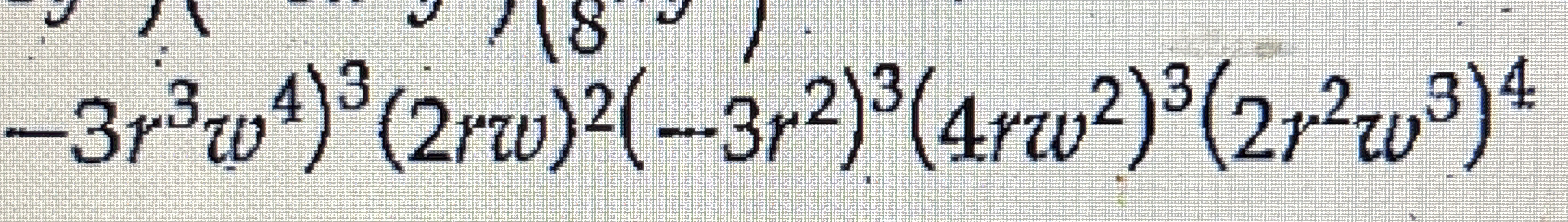
Understand the Problem
The question is presenting a mathematical expression that likely needs to be simplified or solved. It involves several polynomial terms with variables r and w, to the power of different exponents, and may require applying algebraic rules to simplify. This indicates that a detailed step-by-step approach will be needed to handle the exponents and multiplication of these terms.
Answer
The final simplified expression is $$ -36864 r^{20} w^{24} $$.
Answer for screen readers
The final answer is $$ -36864 r^{20} w^{24} $$
Steps to Solve
- Identify the expression's components
We start with the expression: $$ 3r^3w^4(2r^2w)^2(-3r^2)(4rw^2)^3(2r^2w^3)^4 $$ First, we will simplify each term individually.
- Simplify each term
-
For $(2r^2w)^2$: $$ (2r^2w)^2 = 2^2(r^2)^2(w)^2 = 4r^4w^2 $$
-
For $(-3r^2)$, it remains $-3r^2$.
-
For $(4rw^2)^3$: $$ (4rw^2)^3 = 4^3(r)^3(w^2)^3 = 64r^3w^6 $$
-
For $(2r^2w^3)^4$: $$ (2r^2w^3)^4 = 2^4(r^2)^4(w^3)^4 = 16r^8w^{12} $$
- Combine all the simplified terms
Now the expression becomes: $$ 3r^3w^4 \cdot 4r^4w^2 \cdot (-3r^2) \cdot 64r^3w^6 \cdot 16r^8w^{12} $$
- Multiply the coefficients and the variables separately
- Coefficients: $$ 3 \cdot 4 \cdot (-3) \cdot 64 \cdot 16 $$
Calculating that: $$ 3 \cdot 4 = 12 $$ $$ 12 \cdot (-3) = -36 $$ $$ -36 \cdot 64 = -2304 $$ $$ -2304 \cdot 16 = -36864 $$
-
For $r$: $$ r^{3+4+2+3+8} = r^{20} $$
-
For $w$: $$ w^{4+2+6+12} = w^{24} $$
- Final expression
Combining everything: $$ -36864 r^{20} w^{24} $$
The final answer is $$ -36864 r^{20} w^{24} $$
More Information
The coefficient $-36864$ represents the product of all coefficients in the expression, while $r^{20}$ and $w^{24}$ reflect the total powers of variables after simplification. This exercise demonstrates the use of exponent rules and the distributive property in algebra.
Tips
- Forgetting to include the negative sign when simplifying coefficients.
- Miscalculating the power sums for $r$ and $w$. Always double-check each addition.
- Neglecting to simplify each factor fully before multiplication.
AI-generated content may contain errors. Please verify critical information