u(x) = 1 + (1/4) ∫ (cos x * u(t)) dt from 0 to π/2
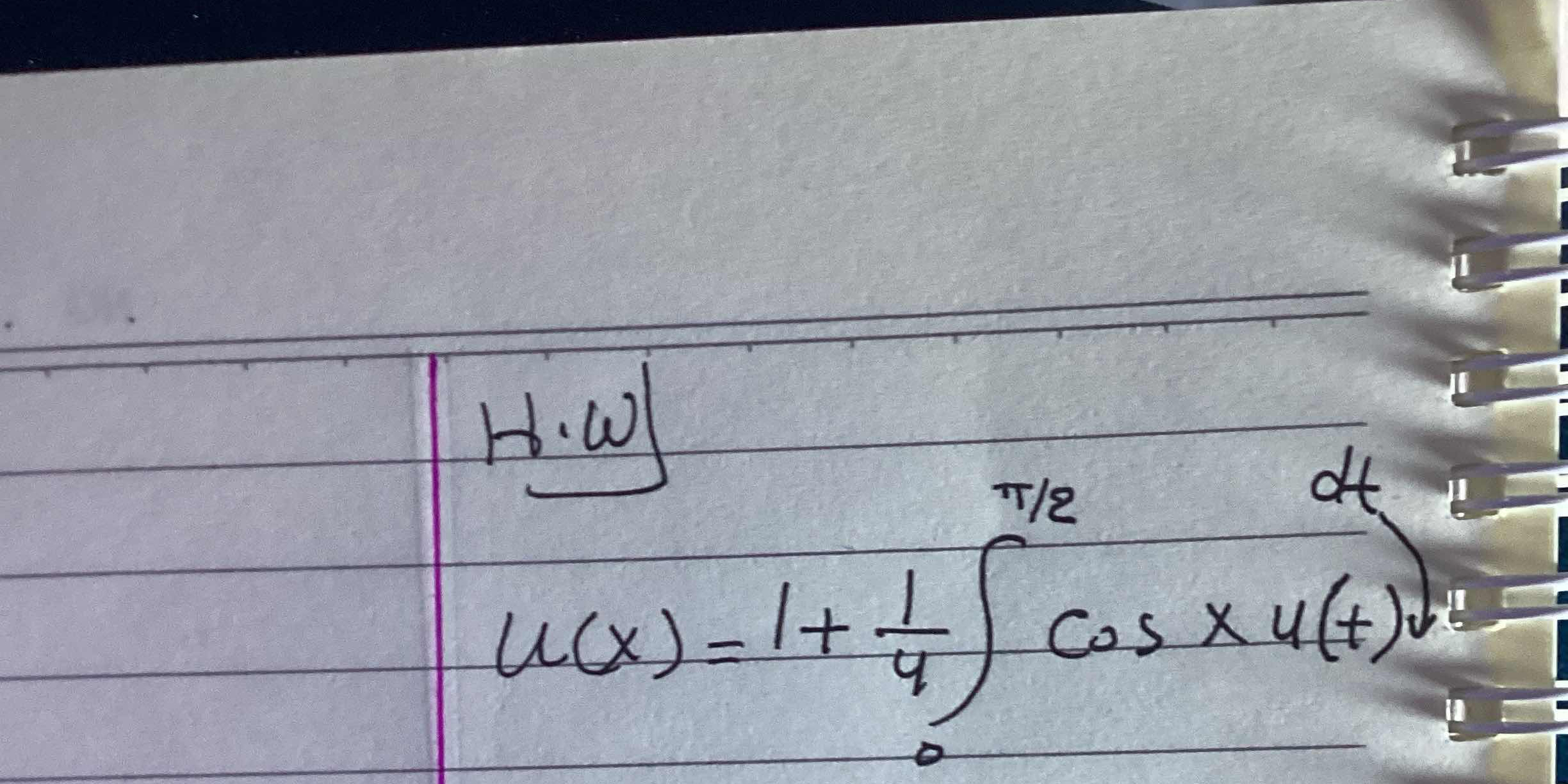
Understand the Problem
The question involves a mathematical function that includes an integral from 0 to π/2 of a product that involves a cosine function and another term involving u(t). The goal is likely to evaluate or manipulate this integral.
Answer
$$ u(x) = 1 + \frac{\pi \cos x}{6} $$
Answer for screen readers
The function is: $$ u(x) = 1 + \frac{\pi \cos x}{6} $$
Steps to Solve
-
Identifying the Given Function The function is defined as: $$ u(x) = 1 + \frac{1}{4} \int_{0}^{\frac{\pi}{2}} \cos x \cdot u(t) , dt $$ Here, $u(x)$ depends on the variable $x$ and involves an integral.
-
Simplifying the Integral Since the integral is independent of the variable $x$, we can factor $\cos x$ out: $$ u(x) = 1 + \frac{\cos x}{4} \int_{0}^{\frac{\pi}{2}} u(t) , dt $$
-
Defining a Constant Let: $$ C = \int_{0}^{\frac{\pi}{2}} u(t) , dt $$ Then, we can rewrite the equation: $$ u(x) = 1 + \frac{\cos x}{4} C $$
-
Finding C by Integration To find $C$, we can substitute back $u(t)$ into the integral: $$ C = \int_{0}^{\frac{\pi}{2}} \left( 1 + \frac{\cos t}{4} C \right) dt $$ Calculate the integral: $$ C = \int_{0}^{\frac{\pi}{2}} 1 , dt + \frac{C}{4} \int_{0}^{\frac{\pi}{2}} \cos t , dt $$
-
Calculating the definite integrals Calculate the first integral: $$ \int_{0}^{\frac{\pi}{2}} 1 , dt = \frac{\pi}{2} $$ Calculate the second integral: $$ \int_{0}^{\frac{\pi}{2}} \cos t , dt = [\sin t]_{0}^{\frac{\pi}{2}} = 1 $$
-
Solving the Equation for C Substituting the values back gives us: $$ C = \frac{\pi}{2} + \frac{C}{4} $$ Multiplying through by 4 to eliminate the fraction: $$ 4C = 2\pi + C $$ Rearranging the terms: $$ 3C = 2\pi $$ Thus, $$ C = \frac{2\pi}{3} $$
-
Final Substitution for u(x) Substituting $C$ back into $u(x)$: $$ u(x) = 1 + \frac{\cos x}{4} \cdot \frac{2\pi}{3} $$ Simplifying gives: $$ u(x) = 1 + \frac{\pi \cos x}{6} $$
The function is: $$ u(x) = 1 + \frac{\pi \cos x}{6} $$
More Information
This function represents a particular solution derived from the initial integral equation. The use of integration and algebraic manipulation helps find the value of $u(x)$, which combines a constant term with a cosine function scaled by the constant $\frac{\pi}{6}$.
Tips
- Failing to recognize that the integral allows for separation of variables.
- Not correctly evaluating the definite integrals.
- Forgetting to substitute back the value of $C$ into the function.
AI-generated content may contain errors. Please verify critical information