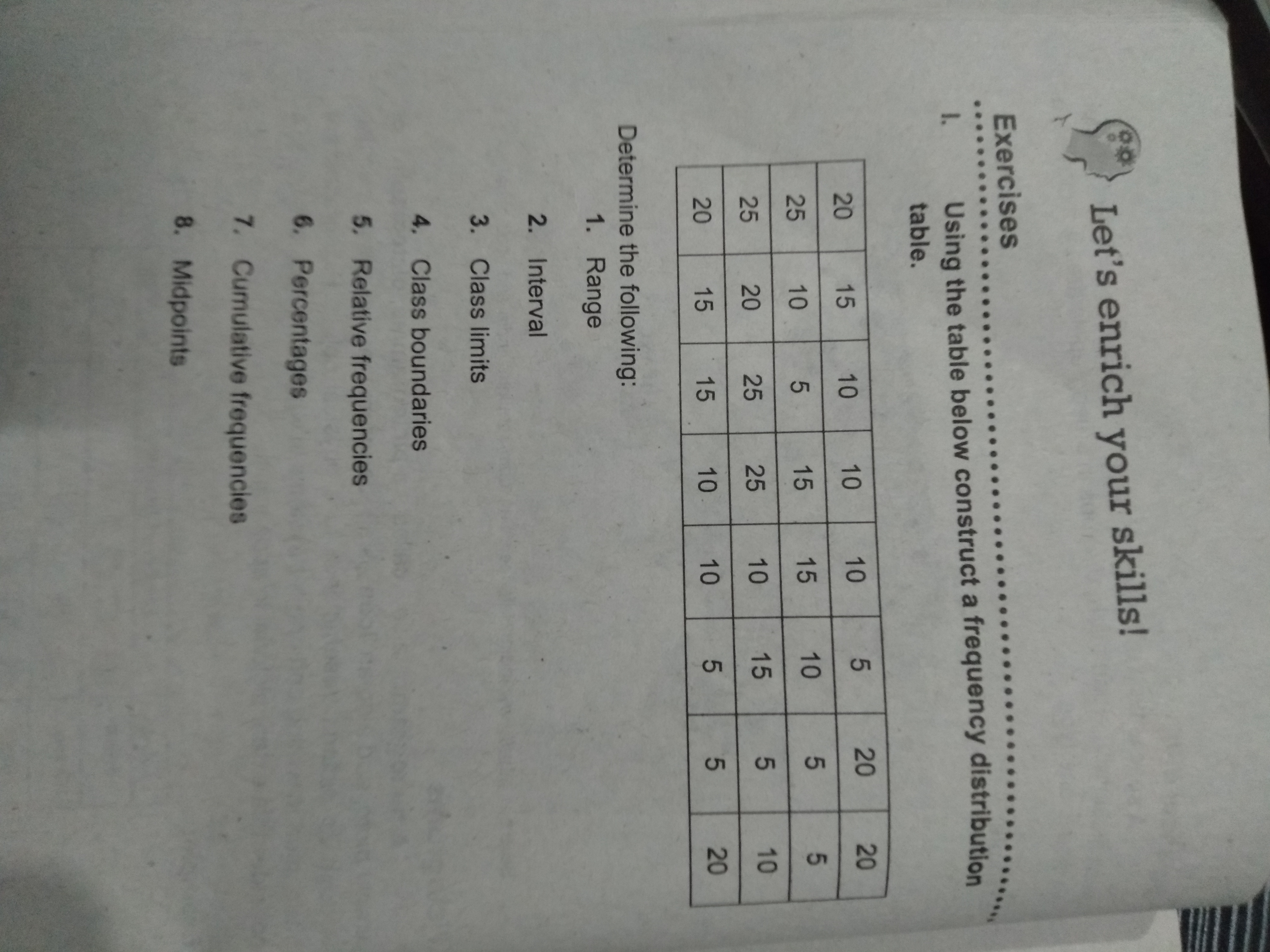
Using the table below, construct a frequency distribution table. Determine the following: 1. Range 2. Interval 3. Class limits 4. Class boundaries 5. Relative frequencies 6. Percen... Using the table below, construct a frequency distribution table. Determine the following: 1. Range 2. Interval 3. Class limits 4. Class boundaries 5. Relative frequencies 6. Percentages 7. Cumulative frequencies 8. Midpoints.

Question image

Understand the Problem

The question is asking for the construction of a frequency distribution table based on the provided data. It includes determining range, interval, class limits, class boundaries, relative frequencies, cumulative frequencies, percentages, and midpoints.

Answer

The range is 20; intervals are 4; class limits are 5-8, 9-12, 13-16, 17-20, 21-24, 25-28; boundaries are 4.5, 28.5; relative frequencies are 0.25, 0.30, 0.20, 0.25, 0.00, 0.00; cumulative frequencies are 5, 11, 15, 20, 20, 20; percentages are 25%, 30%, 20%, 25%, 0%, 0%; midpoints are 6.5, 10.5, 14.5, 18.5, 22.5, 26.5.
Answer for screen readers

Frequency Distribution Table

Class Limits Frequency Relative Frequency Cumulative Frequency Percentage Midpoint
5 - 8 5 0.25 5 25% 6.5
9 - 12 6 0.30 11 30% 10.5
13 - 16 4 0.20 15 20% 14.5
17 - 20 5 0.25 20 25% 18.5
21 - 24 0 0.00 20 0% 22.5
25 - 28 0 0.00 20 0% 26.5

Steps to Solve

  1. Determine the Range The range is calculated as the difference between the highest and lowest values in the data set.

    • Highest value: 25
    • Lowest value: 5
    • Range = Highest - Lowest = $25 - 5 = 20$

  2. Determine the Number of Classes Generally, the number of classes (k) can be calculated using Sturges' formula: $$ k = 1 + 3.322 \log_{10}(n) $$ where ( n ) is the number of observations.

    • Here, ( n = 20 )
    • Therefore, ( k \approx 1 + 3.322 \log_{10}(20) = 5.32 ) (round up to 6 classes)

  3. Calculate the Interval Width The interval width can be found using the formula: $$ \text{Interval Width} = \frac{\text{Range}}{k} = \frac{20}{6} \approx 3.33 $$ Rounding up to the next whole number gives an interval width of 4.

  4. Determine Class Limits and Boundaries Starting from the lowest value (5), the classes can be constructed as follows:

    • Class 1: 5 - 8
    • Class 2: 9 - 12
    • Class 3: 13 - 16
    • Class 4: 17 - 20
    • Class 5: 21 - 24
    • Class 6: 25 - 28

    Class boundaries can be defined as:

    • Lower boundary of Class 1: 4.5
    • Upper boundary of Class 6: 28.5

  5. Tally the Frequencies Count how many data points fall within each class:

    • Class 1 (5-8): 5 occurrences
    • Class 2 (9-12): 6 occurrences
    • Class 3 (13-16): 4 occurrences
    • Class 4 (17-20): 5 occurrences
    • Class 5 (21-24): 0 occurrences
    • Class 6 (25-28): 0 occurrences

  6. Calculate Relative Frequencies The relative frequency is calculated by dividing the frequency of each class by the total number of observations (20):

    • Relative Frequency = $\frac{\text{Frequency}}{n}$
    • Class 1: $\frac{5}{20} = 0.25$
    • Class 2: $\frac{6}{20} = 0.30$
    • Class 3: $\frac{4}{20} = 0.20$
    • Class 4: $\frac{5}{20} = 0.25$
    • Class 5: $\frac{0}{20} = 0.00$
    • Class 6: $\frac{0}{20} = 0.00$

  7. Calculate Cumulative Frequencies Cumulative frequency is the sum of the frequencies for each class and all previous classes:

    • Class 1: 5
    • Class 2: 5 + 6 = 11
    • Class 3: 11 + 4 = 15
    • Class 4: 15 + 5 = 20
    • Class 5: 20 + 0 = 20
    • Class 6: 20 + 0 = 20

  8. Calculate Percentages Percentage is calculated by multiplying the relative frequency by 100:

    • Class 1: $0.25 \times 100 = 25%$
    • Class 2: $0.30 \times 100 = 30%$
    • Class 3: $0.20 \times 100 = 20%$
    • Class 4: $0.25 \times 100 = 25%$
    • Class 5: $0.00 \times 100 = 0%$
    • Class 6: $0.00 \times 100 = 0%$

  9. Calculate Midpoints of Each Class The midpoint is calculated by averaging the class limits:

    • Class 1: $\frac{5 + 8}{2} = 6.5$
    • Class 2: $\frac{9 + 12}{2} = 10.5$
    • Class 3: $\frac{13 + 16}{2} = 14.5$
    • Class 4: $\frac{17 + 20}{2} = 18.5$
    • Class 5: $\frac{21 + 24}{2} = 22.5$
    • Class 6: $\frac{25 + 28}{2} = 26.5$

Frequency Distribution Table

Class Limits Frequency Relative Frequency Cumulative Frequency Percentage Midpoint
5 - 8 5 0.25 5 25% 6.5
9 - 12 6 0.30 11 30% 10.5
13 - 16 4 0.20 15 20% 14.5
17 - 20 5 0.25 20 25% 18.5
21 - 24 0 0.00 20 0% 22.5
25 - 28 0 0.00 20 0% 26.5

More Information

The table summarizes how data can be grouped into classes, facilitating interpretation of distributions. It allows for a clear view of frequencies, relative frequencies, cumulative frequencies, percentages, and midpoints, which are crucial in statistical analysis.

Tips

  • Miscounting Frequencies: It's easy to miscount frequencies when arranging data into classes. Always double-check your tallies.
  • Mistaking Boundaries as Class Limits: Ensure that you understand the difference between class limits and boundaries. Class boundaries help prevent ambiguity at the edges.
  • Incorrect Calculation of Relative Frequencies: Make sure to divide the frequency of each class by the total number of observations accurately.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!
Use Quizgecko on...
Browser
Open
Browser
Browser