Determine the defined range for the equation sin(x) + sin(x)cot(x)^2 = sec(x).
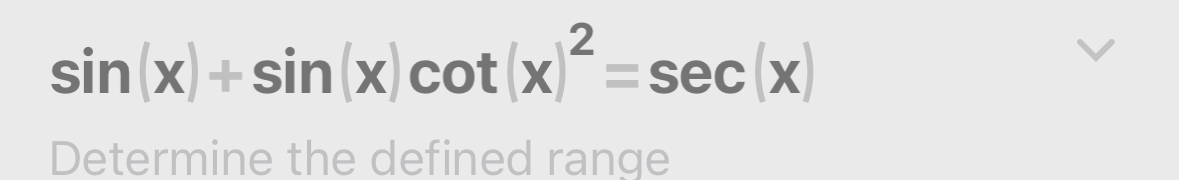
Understand the Problem
The question is asking us to determine the defined range for the equation involving trigonometric functions: sin(x) + sin(x)cot(x)^2 = sec(x). This entails analyzing the equation to find the values of x for which it holds true, considering the domains of the trigonometric functions involved.
Answer
The defined range of \(x\) can be evaluated through numerical or graphical solutions of the derived equation.
Answer for screen readers
The valid range of (x) for which the equation holds true must be checked against the domain limitations of sine and cosine.
Valid intervals can be found through specific evaluations or numerical methods.
Steps to Solve
- Rewrite the Equation First, rewrite the given equation ( \sin(x) + \sin(x) \cot^2(x) = \sec(x) ) using trigonometric identities.
Recall that: [ \cot(x) = \frac{\cos(x)}{\sin(x)} \quad \text{and} \quad \sec(x) = \frac{1}{\cos(x)} ]
-
Express in Terms of Sine and Cosine Substituting the identities into the equation gives: [ \sin(x) + \sin(x) \left(\frac{\cos^2(x)}{\sin^2(x)}\right) = \frac{1}{\cos(x)} ] By simplifying, this becomes: [ \sin(x) + \frac{\cos^2(x)}{\sin(x)} = \frac{1}{\cos(x)} ]
-
Multiply Through by (\sin(x) \cos(x)) To eliminate the denominators, multiply both sides by (\sin(x) \cos(x)): [ \sin^2(x) \cos(x) + \cos^2(x) = \sin(x) ]
-
Rearrange the Equation Rearranging the equation gives: [ \sin^2(x) \cos(x) - \sin(x) + \cos^2(x) = 0 ]
-
Solve for x At this point, we can set up for potential solutions by using numerical methods or graphical methods as the equation doesn't simplify easily into a known function format.
-
Determine the Validity of Solutions Check the solutions of the obtained equation for specified values of (x) where the functions are defined (where (\sin(x) \neq 0) and (\cos(x) \neq 0)) to find the range of function.
The valid range of (x) for which the equation holds true must be checked against the domain limitations of sine and cosine.
Valid intervals can be found through specific evaluations or numerical methods.
More Information
To solve trigonometric equations, we often rely on identities, simplifications, and careful attention to the domains of the functions involved. This particular equation might yield specific solutions, which can be verified numerically or graphically.
Tips
- Ignoring the domain restrictions on sine and cosine can lead to invalid solutions.
- Failing to simplify the expression properly before solving may result in more complex forms that are harder to analyze.
AI-generated content may contain errors. Please verify critical information