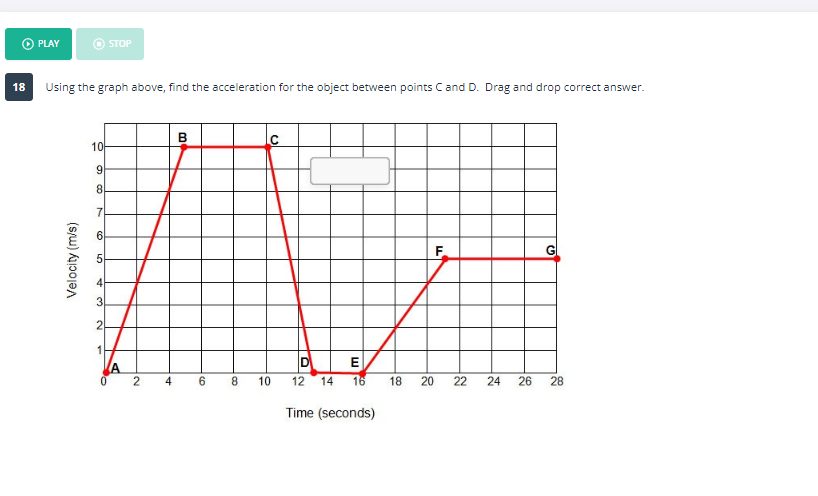
Using the graph above, find the acceleration for the object between points C and D.
Understand the Problem
The question is asking us to calculate the acceleration of an object based on a velocity-time graph between two specific points, C and D. We will need to examine the change in velocity over the time interval to determine the acceleration.
Answer
The acceleration is $a = -1 \, \text{m/s}^2$.
Answer for screen readers
The acceleration of the object between points C and D is $a = -1 , \text{m/s}^2$.
Steps to Solve
- Identify the velocities at points C and D
From the graph, we find the velocity at point C (at 12 seconds) is $v_C = 10 , \text{m/s}$ and the velocity at point D (at 14 seconds) is $v_D = 8 , \text{m/s}$.
- Determine the time interval between C and D
Calculate the time interval $\Delta t$ between points C and D. The time at C is 12 seconds and at D is 14 seconds:
$$ \Delta t = t_D - t_C = 14 , \text{s} - 12 , \text{s} = 2 , \text{s}$$
- Calculate the change in velocity
Determine the change in velocity $\Delta v$ between points C and D:
$$ \Delta v = v_D - v_C = 8 , \text{m/s} - 10 , \text{m/s} = -2 , \text{m/s} $$
- Calculate acceleration
The acceleration $a$ can be calculated using the formula for acceleration:
$$ a = \frac{\Delta v}{\Delta t} $$
Substituting the known values:
$$ a = \frac{-2 , \text{m/s}}{2 , \text{s}} = -1 , \text{m/s}^2 $$
The acceleration of the object between points C and D is $a = -1 , \text{m/s}^2$.
More Information
The negative value of acceleration indicates that the object is slowing down between points C and D, which is consistent with the decrease in velocity observed in the graph.
Tips
- Forgetting to calculate the change in velocity correctly: Ensure to subtract the initial velocity from the final velocity.
- Neglecting the time interval: Always remember to use the correct time frame when calculating acceleration.