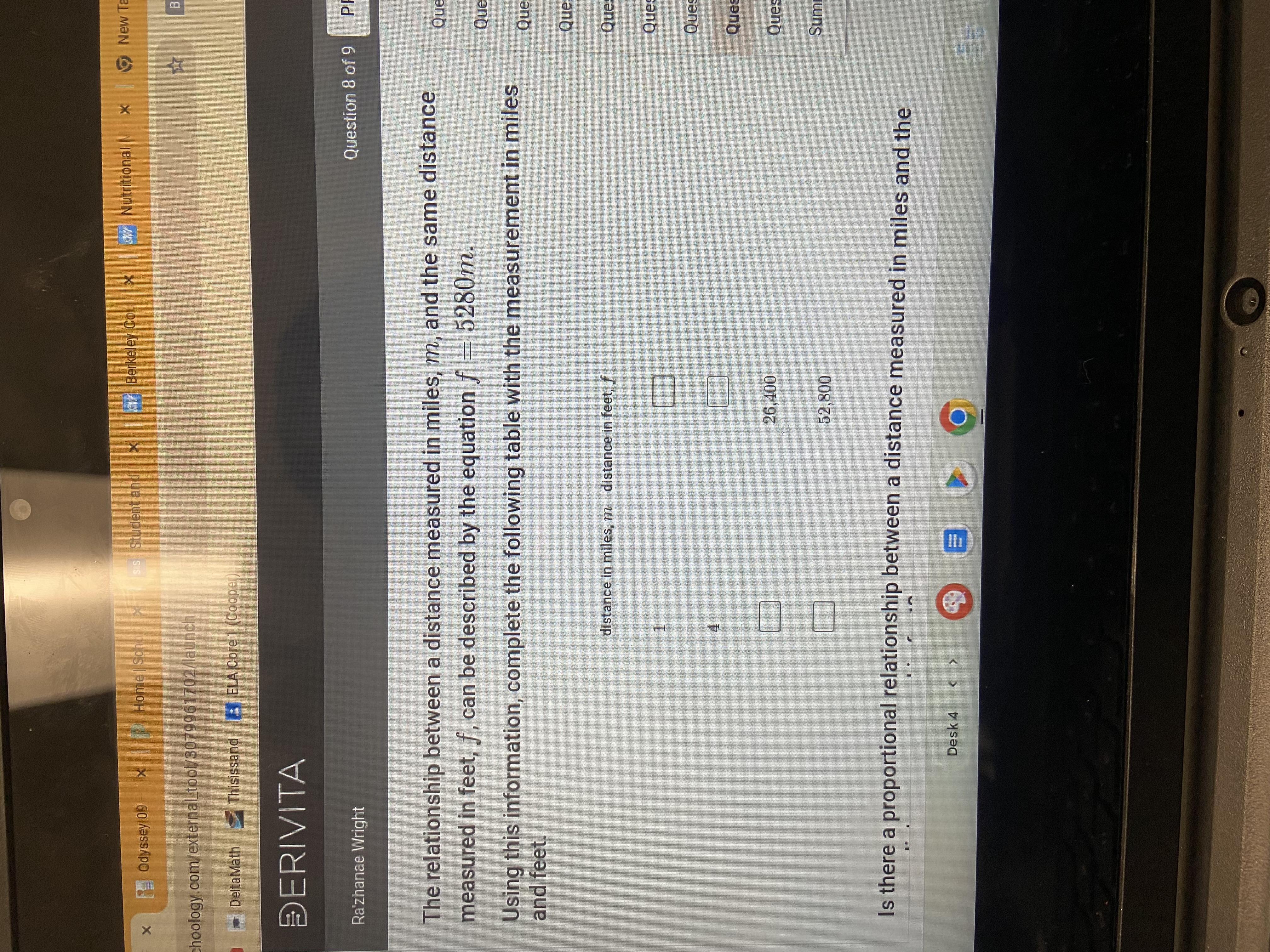
Using the equation f = 5280m, complete the table with the measurement in miles and feet. Is there a proportional relationship between a distance measured in miles and the distance... Using the equation f = 5280m, complete the table with the measurement in miles and feet. Is there a proportional relationship between a distance measured in miles and the distance measured in feet?
Understand the Problem
The question is asking to complete a table that relates distances in miles to corresponding distances in feet using the equation f = 5280m. This involves calculating the distance in feet for given distances in miles and determining if there is a proportional relationship.
Answer
- 5280, 21120, 26400, 52800; Yes.
Answer for screen readers
- For 1 mile: 5280 feet
- For 4 miles: 21120 feet
- Distance in feet for 5 miles: 26400 feet
- Distance in feet for 10 miles: 52800 feet
- Yes, there is a proportional relationship.
Steps to Solve
-
Analyzing the Formula
The formula given is $f = 5280m$, where $f$ is the distance in feet and $m$ is the distance in miles. This means that for every mile, there are 5280 feet. -
Calculating for 1 Mile
To find the distance in feet for 1 mile: $$ f = 5280 \cdot 1 = 5280 \text{ feet} $$ -
Calculating for 4 Miles
Now for 4 miles: $$ f = 5280 \cdot 4 = 21120 \text{ feet} $$ -
Filling in Missing Distances
You already have $26400$ feet and $52800$ feet filled in, so we can solve for the miles by dividing:-
For $26400$ feet: $$ m = \frac{26400}{5280} = 5 \text{ miles} $$
-
For $52800$ feet: $$ m = \frac{52800}{5280} = 10 \text{ miles} $$
-
-
Identifying Proportional Relationship
A proportional relationship exists if the ratio of $f$ to $m$ is constant. Here, the ratio is always $5280$. Therefore, there is a proportional relationship.
- For 1 mile: 5280 feet
- For 4 miles: 21120 feet
- Distance in feet for 5 miles: 26400 feet
- Distance in feet for 10 miles: 52800 feet
- Yes, there is a proportional relationship.
More Information
This problem demonstrates how to convert between miles and feet using a constant factor. It shows that the relationship between the two measurements is linear and proportional, as described by the formula.
Tips
- Forgetting to multiply by $5280$ when converting from miles to feet.
- Miscalculating the division when finding miles from feet.
