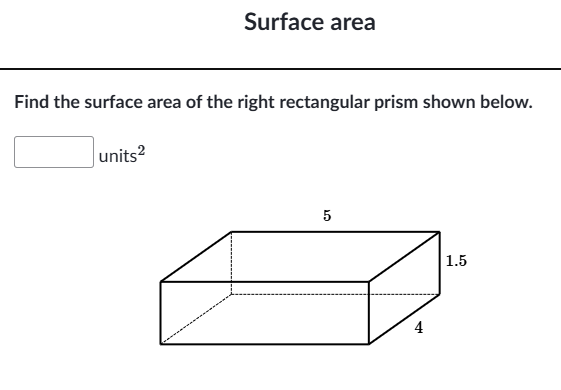
Find the surface area of the right rectangular prism shown below.
Understand the Problem
The question is asking us to find the surface area of a right rectangular prism given its dimensions (length, width, height). We need to apply the formula for the surface area of a rectangular prism.
Answer
The surface area is \( 67 \) units\(^2\).
Answer for screen readers
The surface area of the right rectangular prism is ( 67 ) units(^2).
Steps to Solve
- Identify the dimensions of the prism
From the image, the dimensions of the right rectangular prism are:
- Length ($l$) = 5 units
- Width ($w$) = 4 units
- Height ($h$) = 1.5 units
- Use the formula for surface area
The formula for the surface area ($SA$) of a right rectangular prism is given by: $$ SA = 2(lw + lh + wh) $$
- Calculate the individual products
First, calculate each area:
- $lw = 5 \times 4 = 20$ square units
- $lh = 5 \times 1.5 = 7.5$ square units
- $wh = 4 \times 1.5 = 6$ square units
- Sum the areas
Add the individual products: $$ lw + lh + wh = 20 + 7.5 + 6 = 33.5 $$
- Calculate the surface area
Now, substitute this sum back into the surface area formula: $$ SA = 2(33.5) = 67 $$
The surface area of the right rectangular prism is ( 67 ) units(^2).
More Information
The surface area gives the total area of all the external surfaces of the prism. Understanding surface area is essential in various applications, such as packaging, painting, and material estimation.
Tips
- Forgetting to multiply by 2 in the final step when calculating surface area.
- Misreading the dimensions of the prism—always double-check the labels.
AI-generated content may contain errors. Please verify critical information