Using induction, prove that any non-negative integer can be written as the sum of distinct non-consecutive Lucas numbers.
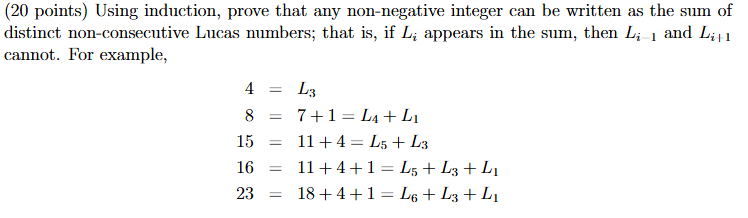
Understand the Problem
The question is asking to prove, using mathematical induction, that any non-negative integer can be expressed as the sum of distinct non-consecutive Lucas numbers. It includes an explanation of the properties of Lucas numbers and provides examples to illustrate how different integers can be represented by sums of these numbers.
Answer
Any non-negative integer can be expressed as the sum of distinct non-consecutive Lucas numbers.
Answer for screen readers
Any non-negative integer can be expressed as the sum of distinct non-consecutive Lucas numbers.
Steps to Solve
-
Base Case: Verifying for n = 0 and n = 1
The Lucas numbers are defined as follows:
- $L_0 = 2$, $L_1 = 1$, $L_2 = 3$, $L_3 = 4$, $L_4 = 7$, $L_5 = 11$, $L_6 = 18$, ...
For $n = 0$: We can express $0$ as the sum of no Lucas numbers, satisfying the condition.
For $n = 1$: We can express $1$ as $L_1$.
Thus, the base cases hold. -
Inductive Hypothesis: Assume the statement is true for all integers up to k
Assume that any non-negative integer $k$ can be expressed as the sum of distinct non-consecutive Lucas numbers. We need to prove it holds for $k + 1$.
-
Inductive Step: Prove for k + 1
Consider $k + 1$. There are two cases:
- If $k + 1$ is equal to a Lucas number, say $L_m$, then it can be represented as itself.
- If $k + 1$ is not a Lucas number, then consider the largest Lucas number less than or equal to $k + 1$, denoted as $L_m$.
We can express $k + 1$ as: $$ k + 1 = (k + 1 - L_m) + L_m $$
By the inductive hypothesis, $(k + 1 - L_m)$ can be expressed as the sum of distinct non-consecutive Lucas numbers. Since $L_{m-1}$ and $L_{m-2}$ are non-consecutive to $L_m$, their inclusion is valid.
-
Conclusion: Combining parts to prove
Thus, we have shown that $k + 1$ can also be represented as the sum of distinct non-consecutive Lucas numbers. Therefore, by the principle of mathematical induction, the statement holds for all non-negative integers.
Any non-negative integer can be expressed as the sum of distinct non-consecutive Lucas numbers.
More Information
The Lucas numbers are similar to Fibonacci numbers, defined by the recurrence relation $L_n = L_{n-1} + L_{n-2}$ with initial conditions $L_0 = 2$ and $L_1 = 1$. This problem connects combinatorial number theory with mathematical induction.
Tips
- Misidentifying Lucas numbers: Ensure that you correctly identify the Lucas numbers up to your target integer.
- Skipping base cases: Always verify the first few integers to establish a strong base case.
- Incorrectly assuming consecutive sums: Distinct non-consecutive means not including both $L_{i-1}$ and $L_i$ simultaneously.
AI-generated content may contain errors. Please verify critical information