Use the table to interpret the rate of change. What is the change for each consecutive input? What is the change for each consecutive output? What is the rate of change for the rel... Use the table to interpret the rate of change. What is the change for each consecutive input? What is the change for each consecutive output? What is the rate of change for the relationship?
Understand the Problem
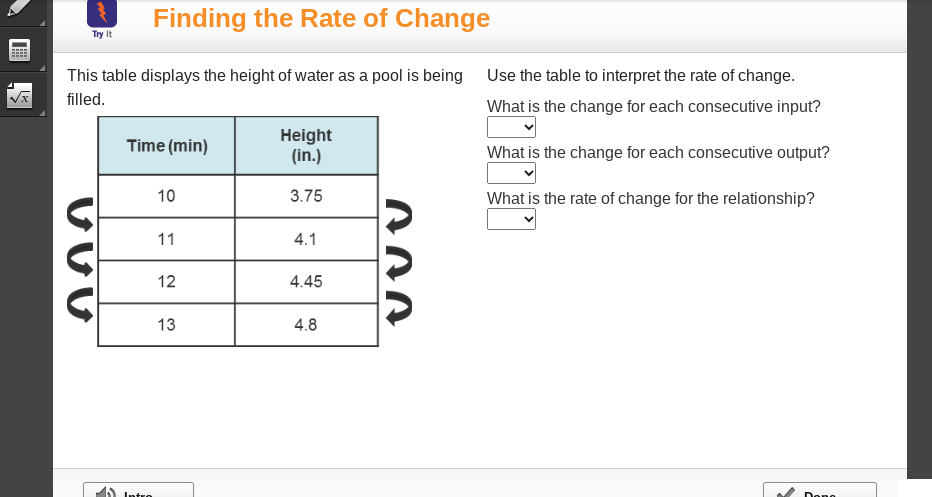
The question is asking to analyze a table showing the height of water in a pool over time and to calculate the rate of change based on the consecutive inputs and outputs provided in the table.
Answer
The rate of change is $0.35$ in/min.
Answer for screen readers
The rate of change for the height of the water in the pool is $0.35$ inches per minute.
Steps to Solve
- Identify the inputs and outputs
From the table, the inputs are the time values in minutes and the outputs are the height of water in inches:
- Time (min): 10, 11, 12, 13
- Height (in.): 3.75, 4.1, 4.45, 4.8
- Calculate the change in inputs (time)
The changes in time for consecutive inputs are:
- From 10 to 11: $11 - 10 = 1$ min
- From 11 to 12: $12 - 11 = 1$ min
- From 12 to 13: $13 - 12 = 1$ min
- Calculate the change in outputs (height)
The changes in height for consecutive outputs are:
- From 10 to 11: $4.1 - 3.75 = 0.35$ in
- From 11 to 12: $4.45 - 4.1 = 0.35$ in
- From 12 to 13: $4.8 - 4.45 = 0.35$ in
- Determine the rate of change
The rate of change can be calculated using the formula:
$$ \text{Rate of Change} = \frac{\text{Change in Output}}{\text{Change in Input}} $$
Using one of the changes: $$ \text{Rate of Change} = \frac{0.35 \text{ in}}{1 \text{ min}} = 0.35 \text{ in/min} $$
The rate of change for the height of the water in the pool is $0.35$ inches per minute.
More Information
The rate of change indicates how quickly the height of the water is increasing as time passes. In this case, the height increases consistently by $0.35$ inches for every minute that passes.
Tips
- Confusing the change in inputs with the change in outputs; make sure to calculate each change separately.
- Not applying the rate of change formula correctly; ensure that you divide the correct output change by the corresponding input change.
AI-generated content may contain errors. Please verify critical information