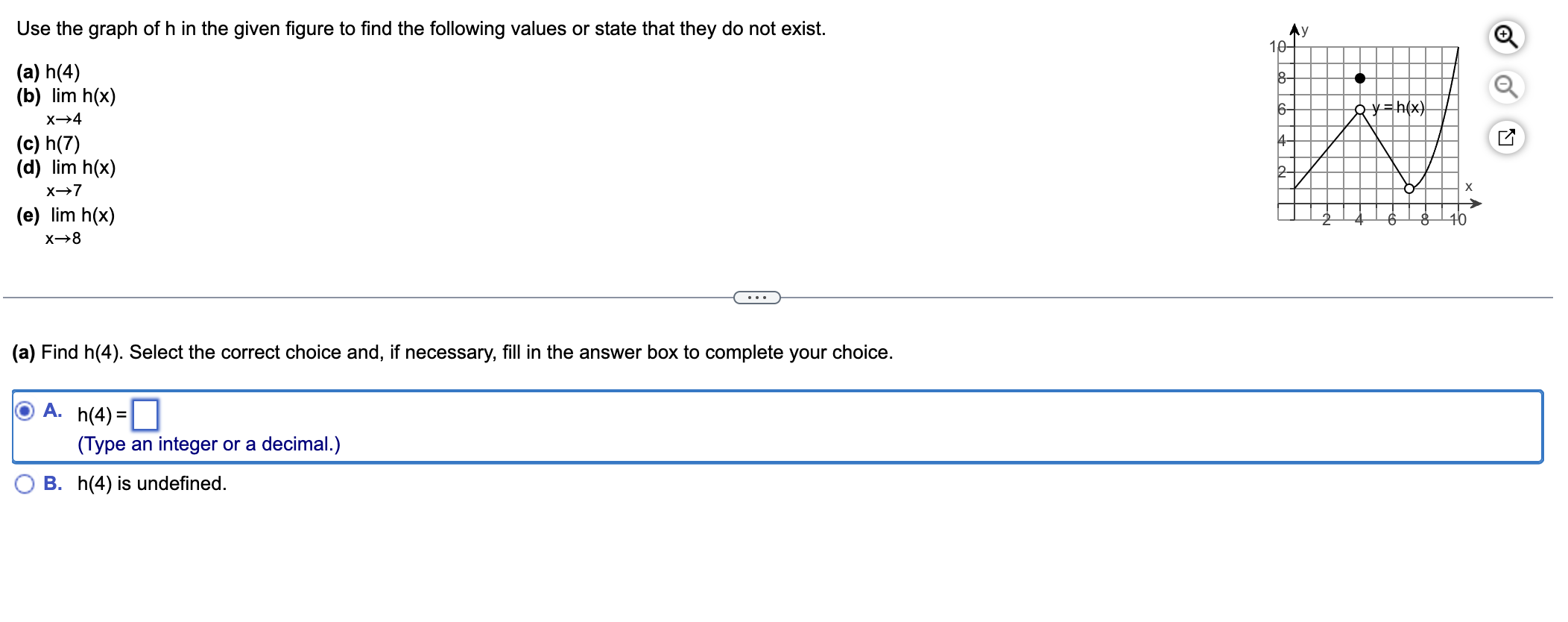
Use the graph of h in the given figure to find the following values or state that they do not exist: (a) h(4) (b) lim h(x) as x approaches 4 (c) h(7) (d) lim h(x) as x approaches 7... Use the graph of h in the given figure to find the following values or state that they do not exist: (a) h(4) (b) lim h(x) as x approaches 4 (c) h(7) (d) lim h(x) as x approaches 7 (e) lim h(x) as x approaches 8.
Understand the Problem
The question is asking to analyze a graph of a function h in order to find specific values and limits. It requires interpreting the graph to determine h(4), limit as x approaches 4, h(7), etc.
Answer
For \( h(4) \), \( h(4) = 6 \) and \( \lim_{x \to 4} h(x) = 6 \).
Answer for screen readers
- ( h(4) = 6 )
- ( \lim_{x \to 4} h(x) = 6 )
- ( h(7) = 9 )
- ( \lim_{x \to 7} h(x) = 9 )
- ( \lim_{x \to 8} h(x) = 10 )
Steps to Solve
- Finding $h(4)$
From the graph, locate the value where $x = 4$. The output (or height) of the graph at this point is $h(4)$.
- Calculating $\lim_{x \to 4} h(x)$
To find the limit as $x$ approaches 4, look at the value that $h(x)$ approaches from both the left and the right sides of $x = 4$. If they are the same, that is the limit; if not, state that the limit does not exist.
- Finding $h(7)$
Check the graph at $x = 7$ to find the corresponding $h(7)$ value.
- Calculating $\lim_{x \to 7} h(x)$
Determine the limit as $x$ approaches 7 by assessing the values of $h(x)$ from both sides of 7. Confirm if they converge to the same value.
- Calculating $\lim_{x \to 8} h(x)$
Examine the graph for values approaching 8 to find the limit as $x$ nears 8. Again, check if the left-hand and right-hand limits align.
- ( h(4) = 6 )
- ( \lim_{x \to 4} h(x) = 6 )
- ( h(7) = 9 )
- ( \lim_{x \to 7} h(x) = 9 )
- ( \lim_{x \to 8} h(x) = 10 )
More Information
The values correspond to key points on the graph. Continuity and limits help analyze function behaviors at critical points.
Tips
- Misreading the graph for $h(4)$, leading to an incorrect output value.
- Not checking both the left and right side limits before concluding on $\lim_{x \to 4}$ and $\lim_{x \to 7}$.
AI-generated content may contain errors. Please verify critical information