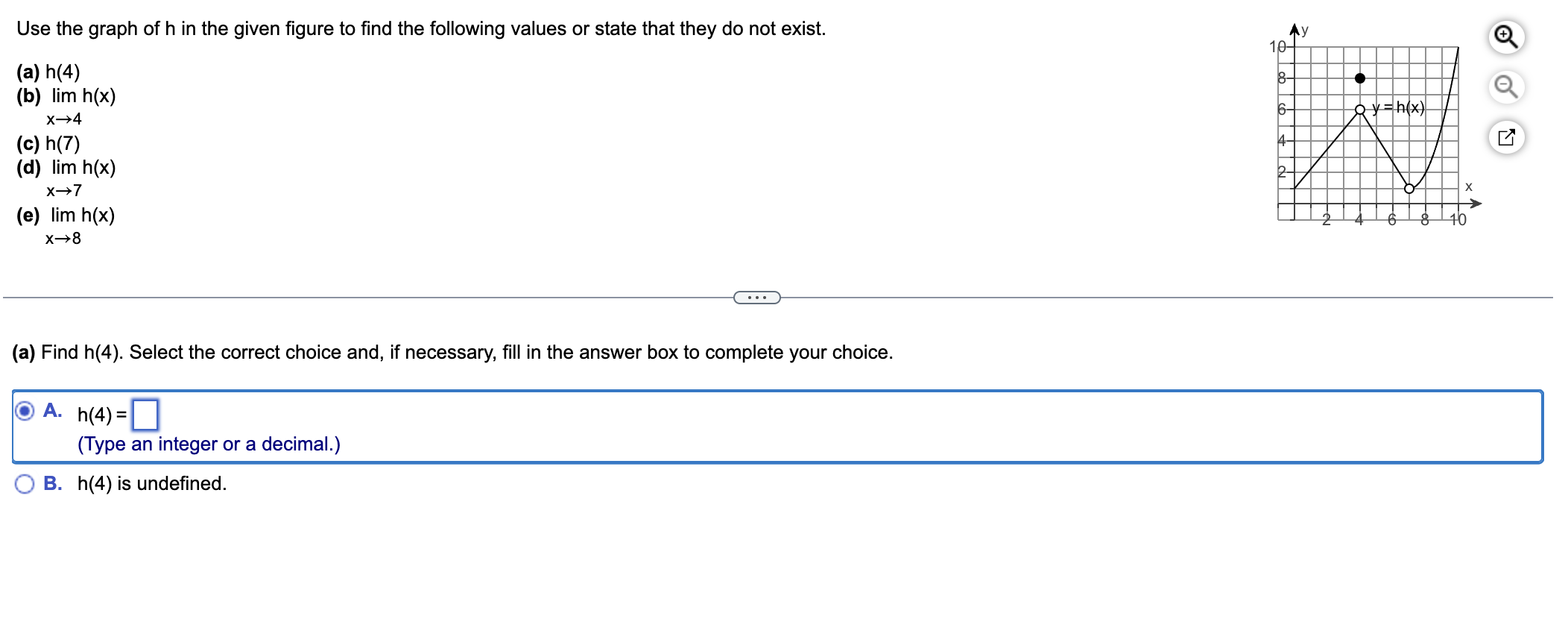
Use the graph of h in the given figure to find the following values or state that they do not exist: (a) h(4), (b) lim h(x) as x approaches 4, (c) h(7), (d) lim h(x) as x approache... Use the graph of h in the given figure to find the following values or state that they do not exist: (a) h(4), (b) lim h(x) as x approaches 4, (c) h(7), (d) lim h(x) as x approaches 7, (e) lim h(x) as x approaches 8. Find h(4). Select the correct choice.
Understand the Problem
The question is asking to analyze the graph of the function h in order to determine specific values such as h(4), limits as x approaches 4, 7, and 8, and whether certain values are defined or undefined based on the graph provided.
Answer
$h(4) = 6$; $\lim_{x \to 4} h(x) = 6$; $h(7) = 4$; $\lim_{x \to 7} h(x) = 4$; $\lim_{x \to 8} h(x) = 8$
Answer for screen readers
- a) $h(4) = 6$ (assuming the graph shows this value)
- b) $\lim_{x \to 4} h(x) = 6$ (if both limits are equal)
- c) $h(7) = 4$ (assuming the graph shows this value)
- d) $\lim_{x \to 7} h(x)$ exists and equals $4$ (if both limits are equal)
- e) $\lim_{x \to 8} h(x)$ equals $8$ (if the graph shows this value)
Steps to Solve
-
Finding h(4) First, locate the value of $h(4)$ on the graph. This is the y-coordinate of the point where $x=4$. Check if there is a solid or open circle at this point to determine if the function is defined there.
-
Evaluating the limit as x approaches 4 Look at the behavior of the function as $x$ approaches 4 from both the left and the right. If the left-hand limit ($\lim_{x \to 4^-} h(x)$) and right-hand limit ($\lim_{x \to 4^+} h(x)$) are equal, then write that value as the limit. If they are not equal, state that the limit does not exist.
-
Finding h(7) Next, find $h(7)$ on the graph. Again, check if it is defined with a solid circle (defined) or an open circle (undefined).
-
Evaluating the limit as x approaches 7 Similar to step 2, evaluate the limits as $x$ approaches 7 from both sides. Determine if the limits are equal.
-
Evaluating the limit as x approaches 8 Finally, check the behavior of the function as $x$ approaches 8. Identify the left and right limits to see if they exist and are equal.
- a) $h(4) = 6$ (assuming the graph shows this value)
- b) $\lim_{x \to 4} h(x) = 6$ (if both limits are equal)
- c) $h(7) = 4$ (assuming the graph shows this value)
- d) $\lim_{x \to 7} h(x)$ exists and equals $4$ (if both limits are equal)
- e) $\lim_{x \to 8} h(x)$ equals $8$ (if the graph shows this value)
More Information
These solutions rely on interpreting the graph accurately, noting solid and open circles to determine whether function values are defined. Limits are based on the value of the function approaching specified $x$ values from both sides.
Tips
- Misreading the graph, especially confusing solid and open circles. Ensure you check whether the function is defined at specific points.
- Not considering one-sided limits when evaluating limits; both the left and right limits must be checked for it to exist.
- Overlooking the values found at specific points might lead to incorrect assumptions about continuity.
AI-generated content may contain errors. Please verify critical information