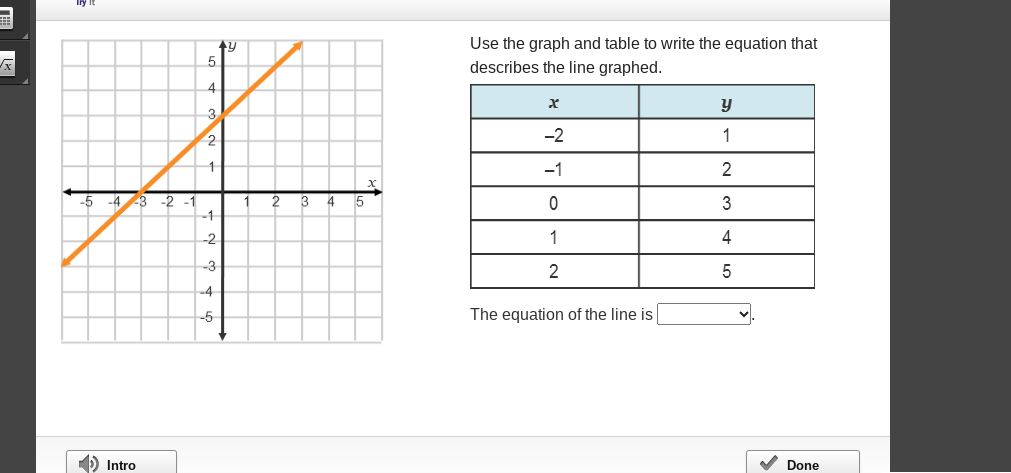
Use the graph and table to write the equation that describes the line graphed.
Understand the Problem
The question is asking to derive the equation of a line based on the provided graph and corresponding table of values. We will use the points in the table to determine the slope and y-intercept of the line.
Answer
The equation of the line is \( y = x + 3 \).
Answer for screen readers
The equation of the line is ( y = x + 3 ).
Steps to Solve
- Identify two points from the table
We can choose two points from the table:
- Point 1: $(-2, 1)$
- Point 2: $(0, 3)$
- Calculate the slope (m) of the line
The formula for the slope between two points $(x_1, y_1)$ and $(x_2, y_2)$ is:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Substituting $(x_1, y_1) = (-2, 1)$ and $(x_2, y_2) = (0, 3)$:
$$ m = \frac{3 - 1}{0 - (-2)} = \frac{2}{2} = 1 $$
- Use the slope-intercept form
The slope-intercept form of a line is given by the equation:
$$ y = mx + b $$
We have found $m = 1$, so the equation now looks like:
$$ y = 1x + b $$
- Determine the y-intercept (b)
To find $b$, we can use one of the points. Using the point $(0, 3)$:
$$ 3 = 1(0) + b \implies b = 3 $$
- Write the final equation
Substituting the values of $m$ and $b$ back into the equation:
$$ y = 1x + 3 $$
This simplifies to:
$$ y = x + 3 $$
The equation of the line is ( y = x + 3 ).
More Information
This equation represents a line with a slope of 1, which means that for every 1 unit increase in ( x ), ( y ) increases by 1 unit. The y-intercept at ( (0, 3) ) indicates where the line crosses the y-axis.
Tips
- Incorrectly identifying points: Make sure to accurately read the coordinates from the table.
- Mistaking slope calculation: Remember that the slope is the rise over run; be careful with subtraction in the slope formula.
- Forgetting to substitute properly: Ensure that when you find ( b ), you correctly substitute the point values into the equation.
AI-generated content may contain errors. Please verify critical information