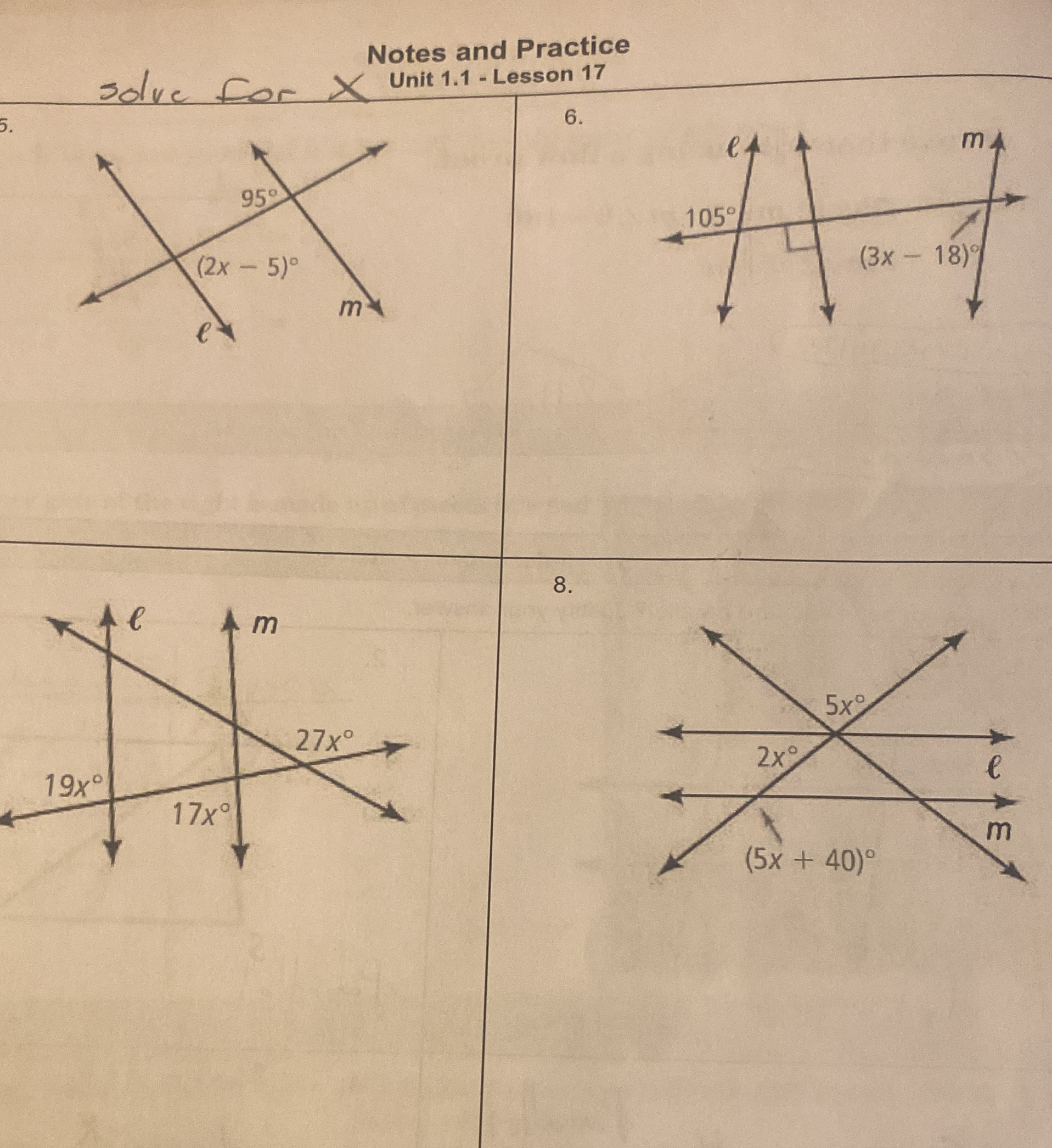
Solve for x in the given angle relationships.
Understand the Problem
The question involves solving for the variable 'x' in various angle relationships illustrated by intersecting lines. Specifically, it requires finding the values of 'x' based on angle measures formed by these intersections.
Answer
- Problem 5: $x = 45$ - Problem 6: $x = 41$ - Problem 7: $x = 1$ - Problem 8: $x = 8$
Answer for screen readers
- Problem 5: $x = 45$
- Problem 6: $x = 41$
- Problem 7: $x = 1$
- Problem 8: $x = 8$
Steps to Solve
-
Identify angle relationships In each diagram, identify corresponding, alternate interior, or vertically opposite angles formed by intersecting lines.
-
Set up equations For each problem, set up an equation based on the angle relationships.
- For example, in Problem 5, you can write: $$ 95^\circ + (2x - 5)^\circ = 180^\circ $$ since they are supplementary angles.
- Solve for x Isolate the variable 'x' in your equation.
- Continuing with Problem 5: $$ 95 + 2x - 5 = 180 $$ Simplifying gives: $$ 2x + 90 = 180 $$ Next, subtract 90 from both sides: $$ 2x = 90 $$ Lastly, divide by 2: $$ x = 45 $$
-
Repeat for other problems Use similar steps to solve Problems 6, 7, and 8 by identifying the relationships and solving accordingly.
-
Double-check your answers After calculating 'x' for each problem, verify that the angle measures satisfy the angle relationships.
- Problem 5: $x = 45$
- Problem 6: $x = 41$
- Problem 7: $x = 1$
- Problem 8: $x = 8$
More Information
The problems explore relationships between angles formed by intersecting lines, leveraging properties like supplementary and vertically opposite angles to solve for 'x'.
Tips
- Forgetting that angles formed by intersecting lines can be supplementary or equal.
- Not carefully simplifying equations, leading to calculation errors.
- Misidentifying which angles correspond to each other when setting up equations.
AI-generated content may contain errors. Please verify critical information