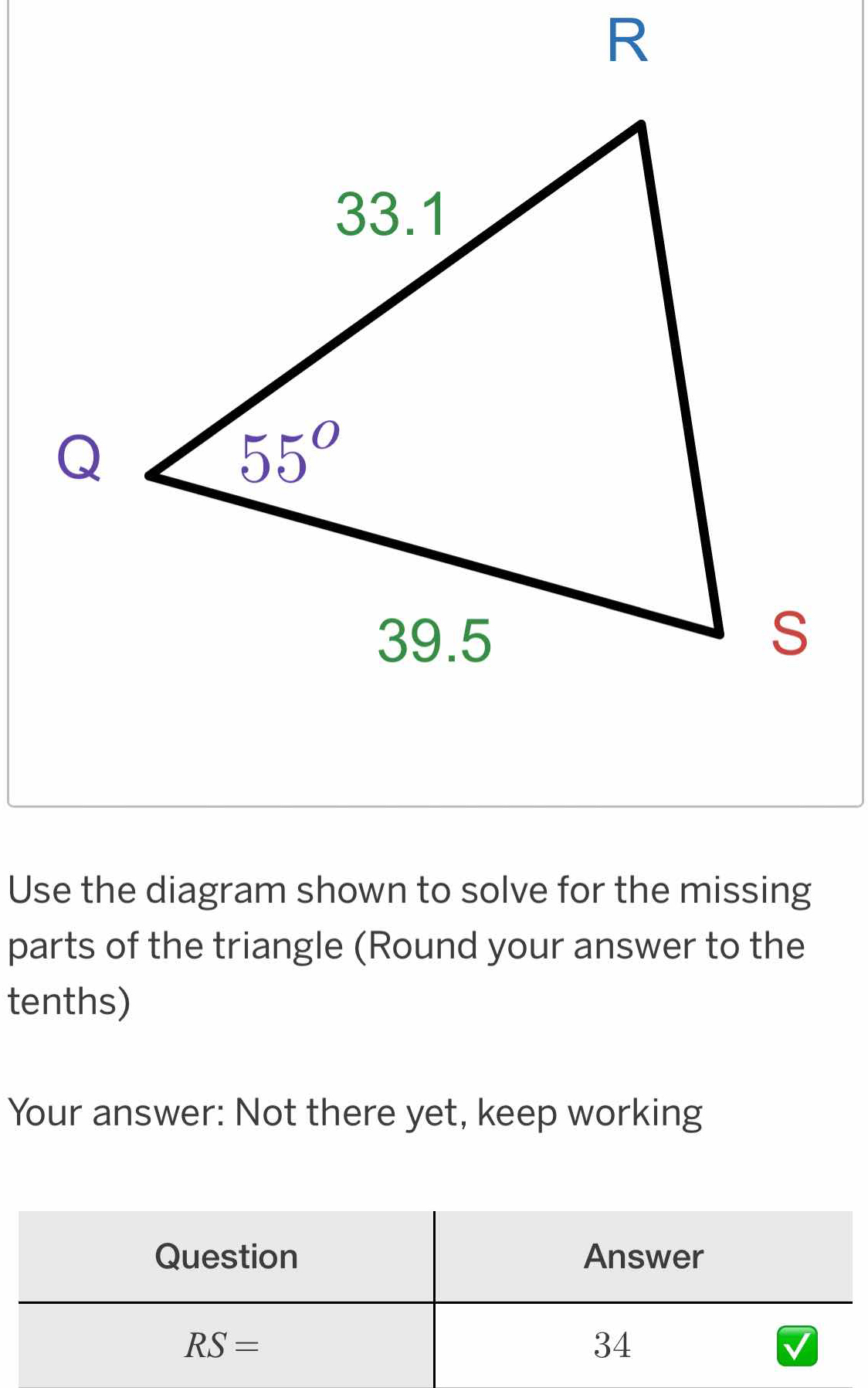
Use the diagram shown to solve for the missing parts of the triangle. What is the length of RS?

Steps to Solve

1. Identify known values The given information includes:

• Angle $Q = 55^\circ$
• Side $QS = 39.5$
• Side $QR = 33.1$

2. Calculate the missing angle Using the triangle sum property, the sum of angles in a triangle equals $180^\circ$. Thus, we find angle $R$: $$ R = 180^\circ - Q - S $$ Where $S$ can be found later. First, we need to calculate angle $S$.

3. Use the Law of Sines We can set up the Law of Sines to relate the sides and angles: $$ \frac{QS}{\sin R} = \frac{QR}{\sin Q} $$

4. Substitute and rearrange Substituting the known sides and angles into the equation: $$ \frac{39.5}{\sin R} = \frac{33.1}{\sin(55^\circ)} $$

5. Solve for $R$ Isolate $\sin R$: $$ \sin R = \frac{39.5 \cdot \sin(55^\circ)}{33.1} $$

6. Calculate angle $R$ Use a calculator to find $R$: $$ R = \arcsin\left(\frac{39.5 \cdot \sin(55^\circ)}{33.1}\right) $$

7. Determine missing angle $S$ Now we can find angle $S$ using: $$ S = 180^\circ - 55^\circ - R $$

8. Use Law of Sines again to find side $RS$ Finally, apply the Law of Sines again for side $RS$: $$ \frac{RS}{\sin S} = \frac{39.5}{\sin(55^\circ)} $$

9. Solve for $RS$ Rearranging gives: $$ RS = \frac{39.5 \cdot \sin S}{\sin(55^\circ)} $$