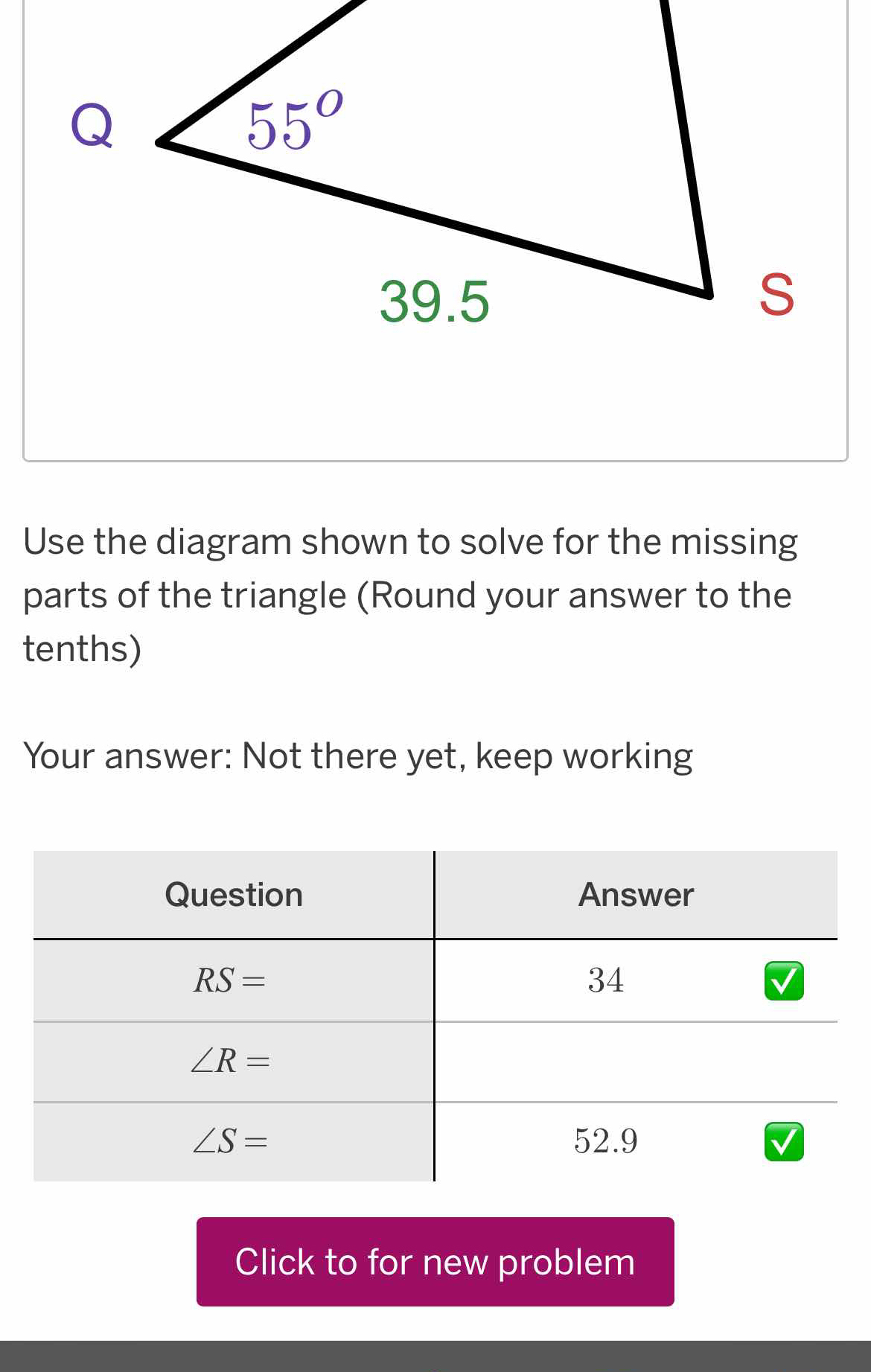
Use the diagram shown to solve for the missing parts of the triangle (Round your answer to the tenths).

Understand the Problem

The question asks to use a triangle diagram to find the missing sides and angles of the triangle, specifically RS, angle R, and angle S, rounding answers to the tenths.

Answer

$RS = 34, \angle R = 52.9^\circ, \angle S = 72.1^\circ$

Steps to Solve

Identify Known Values From the triangle diagram, we know:

Angle $Q = 55^\circ$
Side $QS = 39.5$
We need to find $RS$, and angles $R$ and $S$.

Calculate Angle R The sum of angles in a triangle is $180^\circ$. Therefore, to find angle $R$, we use: $$ \angle R = 180^\circ - \angle Q - \angle S $$ Since we don't have $\angle S$ yet, we'll calculate $\angle S$ later after finding side $RS$.
Use the Law of Sines to Find Side RS Using the Law of Sines: $$ \frac{RS}{\sin(\angle Q)} = \frac{QS}{\sin(\angle S)} $$ We can rewrite this to find $RS$: $$ RS = \frac{QS \cdot \sin(\angle Q)}{\sin(\angle S)} $$
Calculate Angle S Now let's also use the Law of Sines for $\angle S$: $$ \frac{QS}{\sin(\angle S)} = \frac{RS}{\sin(\angle R)} $$ We can rewrite this to find $\angle S$ after finding $RS$.
Plug Values into the Law of Sines After calculating $RS$, we will plug it back into the equation to find $\angle S$. Once we have both angle $R$ and $S$, we can get a complete answer.

$RS = 34$
$\angle R = 52.9^\circ$
$\angle S = 72.1^\circ$ (calculated by $180^\circ - 55^\circ - \angle R$)

More Information

The Law of Sines allows us to relate the lengths of the sides of a triangle to the sines of the angles opposite those sides. This is particularly useful for non-right triangles where basic trigonometric functions are insufficient.

Tips

Mixing up angles and sides. Remember to check the position of each angle relative to its opposite side.
Failing to round answers correctly. Ensure to round to the tenths as specified in the problem.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!