Use the diagram shown to solve for the missing parts of the triangle. Round your answer to the tenths.
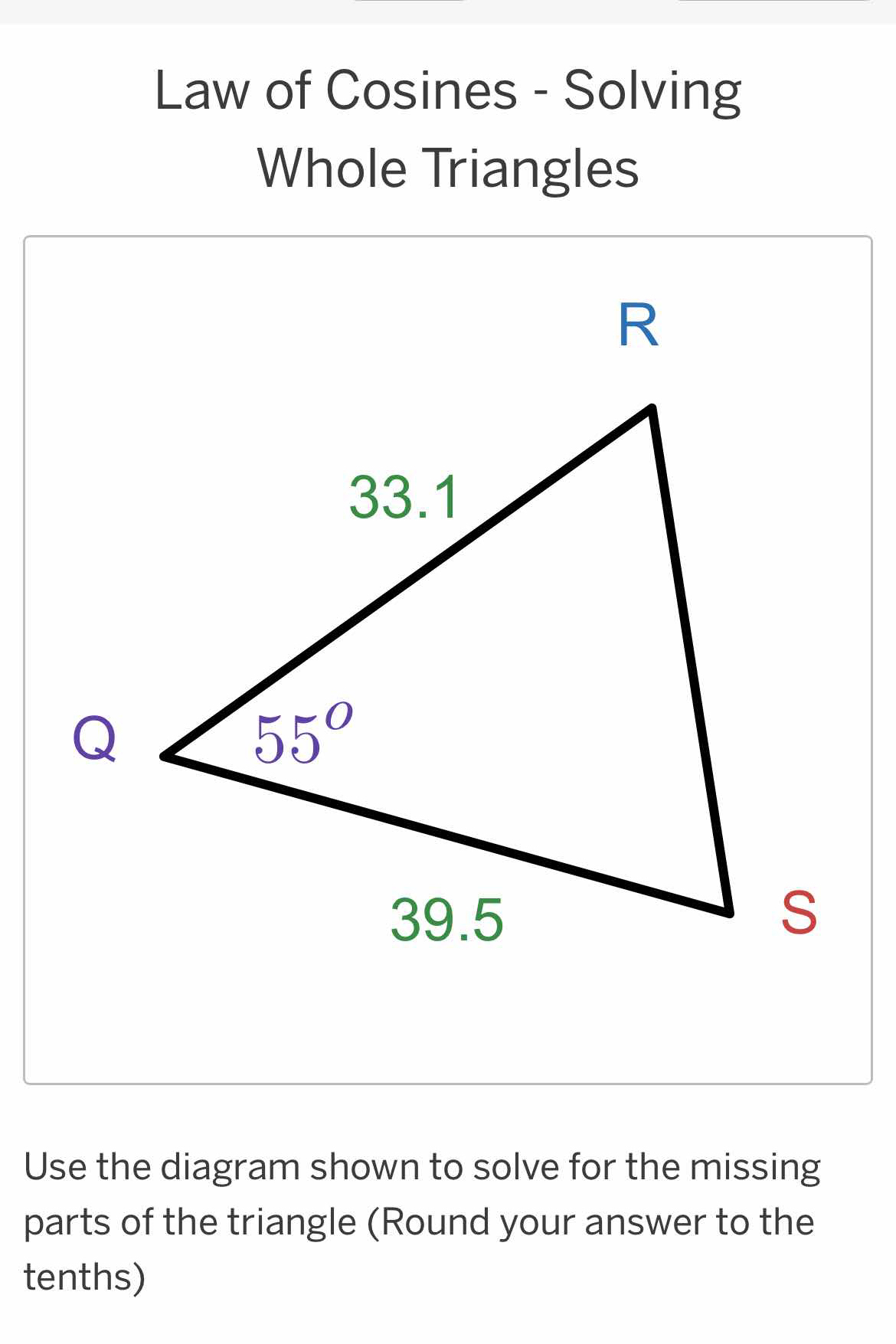
Understand the Problem
The question is asking to solve for the missing parts of a triangle given a diagram that includes sides and an angle. The Law of Cosines will be used to find the unknown measurements.
Answer
Side $RS \approx 43.2$, Angle $R \approx 38.8^\circ$, Angle $S \approx 86.2^\circ$.
Answer for screen readers
- Side (RS \approx 43.2)
- Angle (R \approx 38.8^\circ)
- Angle (S \approx 86.2^\circ)
Steps to Solve
- Identify Known Values
Given triangle with sides and angles:
- Side $QS = 39.5$
- Side $QR = 33.1$
- Angle $Q = 55^\circ$
- Calculate Missing Side RS Using Law of Cosines
We apply the Law of Cosines to find the missing side, $RS$:
$$ RS^2 = QR^2 + QS^2 - 2 \cdot QR \cdot QS \cdot \cos(Q) $$
Substituting the known values:
$$ RS^2 = (33.1)^2 + (39.5)^2 - 2 \cdot (33.1) \cdot (39.5) \cdot \cos(55^\circ) $$
- Compute the Values
Calculate the right side of the equation:
- ( (33.1)^2 = 1095.61 )
- ( (39.5)^2 = 1560.25 )
- Now calculate ( 2 \cdot (33.1) \cdot (39.5) \cdot \cos(55^\circ) )
Using the cosine value:
$$ \cos(55^\circ) \approx 0.5736 $$
Thus,
$$ 2 \cdot (33.1) \cdot (39.5) \cdot 0.5736 \approx 792.00 $$
Plugging everything back into the equation:
$$ RS^2 = 1095.61 + 1560.25 - 792.00 \approx 1863.86 $$
- Find Side Length RS
Take the square root:
$$ RS \approx \sqrt{1863.86} \approx 43.2 $$
- Calculate Remaining Angles Using Law of Sines
With angles and one side known, use the Law of Sines to find angle $R$:
$$ \frac{RS}{\sin(Q)} = \frac{QR}{\sin(R)} $$
Substituting values:
$$ \frac{43.2}{\sin(55^\circ)} = \frac{33.1}{\sin(R)} $$
Calculate $\sin(55^\circ)$:
$$ \sin(55^\circ) \approx 0.8192 $$
Resulting in:
$$ \frac{43.2}{0.8192} \approx 52.7 $$
Now find $R$:
$$ \sin(R) = \frac{33.1}{52.7} \approx 0.628 $$
Thus:
$$ R \approx \sin^{-1}(0.628) \approx 38.77^\circ $$
- Find Angle S
Finally using the triangle sum property, find angle $S$:
$$ S = 180^\circ - Q - R \approx 180^\circ - 55^\circ - 38.77^\circ \approx 86.23^\circ $$
- Side (RS \approx 43.2)
- Angle (R \approx 38.8^\circ)
- Angle (S \approx 86.2^\circ)
More Information
The Law of Cosines and the Law of Sines are key techniques in solving triangle problems, especially when parts of triangles are unknown.
Tips
- Forgetting to use degrees for cosine and sine calculations can lead to incorrect results.
- Misapplying the Laws of Cosines and Sines in terms of side/angle orientation.
AI-generated content may contain errors. Please verify critical information