4(c - 72) + 3 = 93 - c
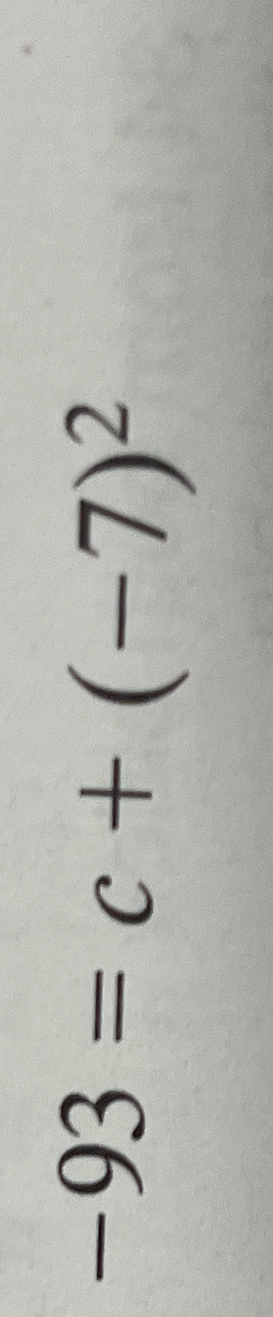
Understand the Problem
The question appears to involve solving an equation, likely pertaining to algebra, which includes variables and constants. The equation will need to be rearranged to isolate the variable and find its value.
Answer
\( c = 75.6 \)
Answer for screen readers
The solution is ( c = 75.6 ).
Steps to Solve
-
Distribute the multiplication
First, distribute the $4$ across the parenthesis:
$$ 4(c - 72) = 4c - 288 $$ -
Rewrite the equation
Now, rewrite the original equation with the distributed terms:
$$ 4c - 288 + 3 = 93 - c $$ -
Combine like terms
Combine the constant terms on the left side:
$$ 4c - 285 = 93 - c $$ -
Isolate the variable
Add $c$ to both sides to bring all variable terms to one side of the equation:
$$ 4c + c - 285 = 93 $$
This simplifies to:
$$ 5c - 285 = 93 $$ -
Add 285 to both sides
Next, add $285$ to both sides to isolate the term with $c$:
$$ 5c = 93 + 285 $$
This simplifies to:
$$ 5c = 378 $$ -
Solve for $c$
Finally, divide both sides by $5$ to solve for $c$:
$$ c = \frac{378}{5} $$
This can also be written as:
$$ c = 75.6 $$
The solution is ( c = 75.6 ).
More Information
The solution obtained, ( c = 75.6 ), is a decimal value indicating that the variable ( c ) can take on non-integer values. In practical terms, such variables might be used in various applications, including financial calculations, measurements, or other scenarios requiring precision.
Tips
- Forgetting to distribute the multiplication correctly.
- Combining terms inaccurately, especially constants on different sides of the equation.
- Not isolating the variable step-by-step, which can lead to confusion.
AI-generated content may contain errors. Please verify critical information