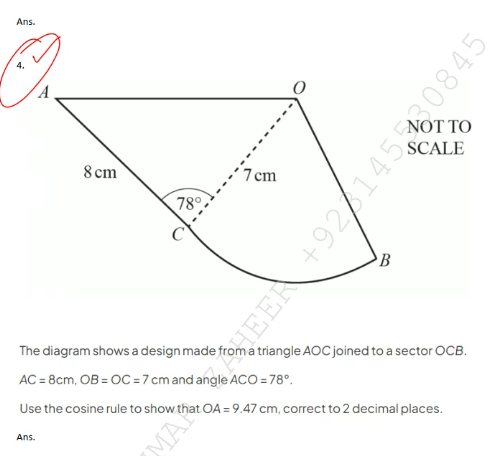
Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.

Steps to Solve

1. Identify the given values We have the following measurements:

• $AC = 8$ cm
• $OC = 7$ cm
• The angle $ACO = 78^\circ$

2. Apply the cosine rule The cosine rule states that for a triangle with sides $a$, $b$, and $c$, and respective opposite angles $A$, $B$, and $C$: $$ c^2 = a^2 + b^2 - 2ab \cos(C) $$

For triangle AOC, we need to find $OA$. Let's set:

• $AC = b = 8 \text{ cm}$
• $OC = a = 7 \text{ cm}$
• Angle $ACO = C = 78^\circ$
• Side $OA = c$ (what we want to find)

3. Plug the values into the cosine rule formula Using the values from the previous step:
   $$ OA^2 = AC^2 + OC^2 - 2 \cdot AC \cdot OC \cdot \cos(78^\circ) $$

Replacing with the known values: $$ OA^2 = 8^2 + 7^2 - 2 \cdot 8 \cdot 7 \cdot \cos(78^\circ) $$

4. Calculate the squares and the cosine First, calculate $8^2$ and $7^2$: $$ 8^2 = 64 $$ $$ 7^2 = 49 $$ Now, calculate: $$ OA^2 = 64 + 49 - 2 \cdot 8 \cdot 7 \cdot \cos(78^\circ) $$

5. Use the calculator to find $\cos(78^\circ)$ and finalize the calculation From a calculator: $$ \cos(78^\circ) \approx 0.2079 $$

Now substitute this into the equation: $$ OA^2 = 64 + 49 - 2 \cdot 8 \cdot 7 \cdot 0.2079 $$

Calculating further: $$ OA^2 = 113 - 2 \cdot 8 \cdot 7 \cdot 0.2079 $$ $$ OA^2 = 113 - 23.3888 $$

6. Now, solve for OA Finally, calculate: $$ OA^2 \approx 89.6112 $$ $$ OA \approx \sqrt{89.6112} \approx 9.47 \text{ cm} $$