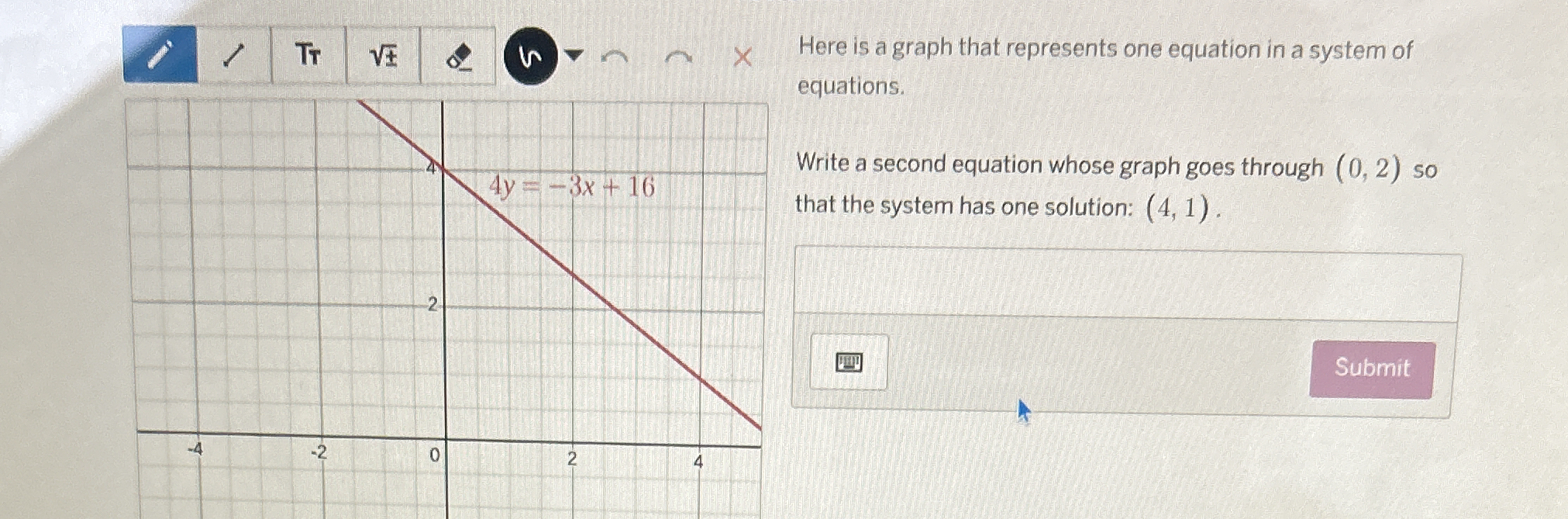
Write a second equation whose graph goes through (0, 2) so that the system has one solution: (4, 1).

Steps to Solve

1. Identify the given equation and the point of intersection

The given equation is:

$$ 4y = -3x + 16 $$

We want to find a second equation that passes through the point $(0, 2)$ and intersects the above equation at the point $(4, 1)$.

2. Find the slope of the given equation

First, let's rearrange the given equation into slope-intercept form (i.e., $y = mx + b$):

[ y = -\frac{3}{4}x + 4 ]

Here, the slope ($m_1$) is $-\frac{3}{4}$.

3. Determine the slope of the new line

Since we want the new equation to intersect the given line at $(4, 1)$, we'll set the second line's slope ($m_2$) to be different to ensure one solution.

From point $(0, 2)$ to $(4, 1)$, the slope can be calculated as:

$$ m_2 = \frac{1 - 2}{4 - 0} = -\frac{1}{4} $$

4. Write the equation using point-slope form

Using the point-slope form of a line:

$$ y - y_1 = m(x - x_1) $$

Here, $(x_1, y_1) = (0, 2)$ and $m = -\frac{1}{4}$:

[ y - 2 = -\frac{1}{4}(x - 0) ]

5. Rearranging the equation

Now, rearranging it into slope-intercept form, we get:

[ y - 2 = -\frac{1}{4}x ] [ y = -\frac{1}{4}x + 2 ]

This is the second equation.