Use bracket notation to give the set {n ∈ N | n > 3} - {n ∈ Z | n < 5} in a finite listed form.
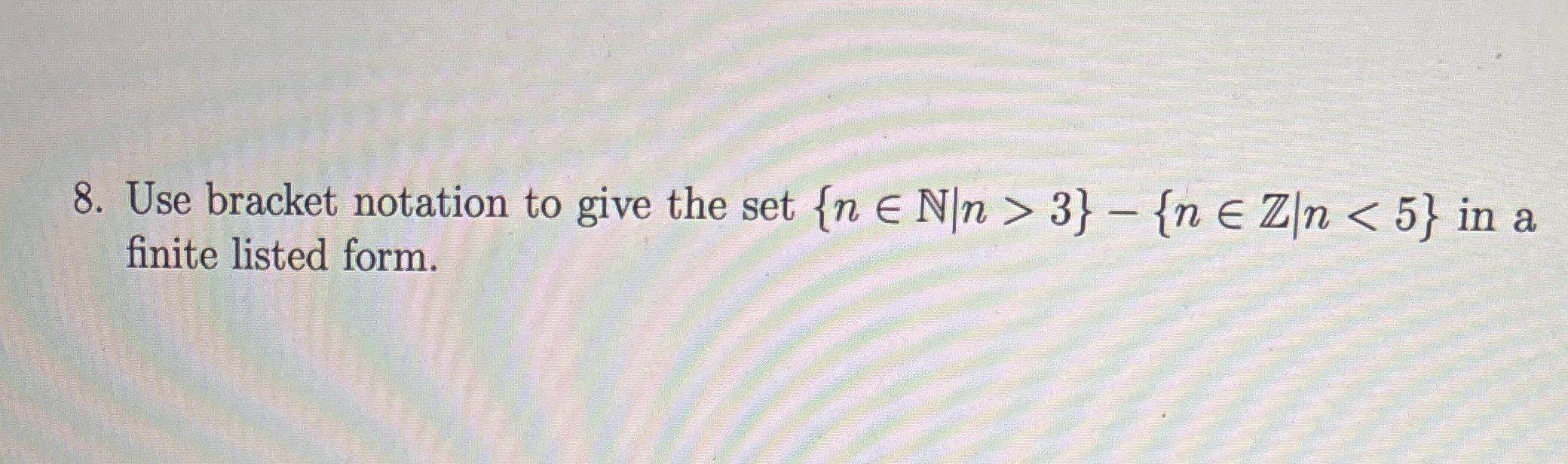
Understand the Problem
The question requires us to define a set using bracket notation by performing the specified set operations: include natural numbers greater than 3 and exclude integers less than 5.
Answer
The set is given by: $$ \{ 5, 6, 7, 8, 9, 10 \} $$
Answer for screen readers
The set in finite listed form is: $$ { 5, 6, 7, 8, 9, 10 } $$
Steps to Solve
-
Identify the First Set Definition We need to define the first set: $$ A = { n \in \mathbb{N} \mid n > 3 } $$ This set consists of all natural numbers greater than 3. Therefore, the elements are: $$ A = { 4, 5, 6, 7, 8, \ldots } $$
-
Identify the Second Set Definition Now, we define the second set: $$ B = { n \in \mathbb{Z} \mid n < 5 } $$ This set includes all integers less than 5. So, the elements are: $$ B = { \ldots, -2, -1, 0, 1, 2, 3, 4 } $$
-
Find the Set Difference The problem requires us to find the difference: $$ A - B $$ This means we will remove all elements in set B from set A. Since set A includes natural numbers starting from 4, we will exclude the integers 4 (since it's the only relevant element in B).
The elements in A are (4, 5, 6, 7, \ldots), removing 4 gives us: $$ A - B = { 5, 6, 7, 8, \ldots } $$
-
Express the Result in Finite Listed Form Since the problem requests a finite form, we can represent this as: $$ A - B = { 5, 6, 7, 8, 9, 10 } $$ Here, we limit the representation to a few numbers for clarity.
The set in finite listed form is: $$ { 5, 6, 7, 8, 9, 10 } $$
More Information
The set $A - B$ represents natural numbers greater than 3 after excluding those integers less than 5. Since natural numbers start from 1, excluding the integers below 5 means we focus on numbers from 5 upwards.
Tips
- Confusing natural numbers with integers: Remember that natural numbers start from 1, while integers can include negative numbers and zero.
- Forgetting to exclude elements from the first set based on the second set: Always check both sets carefully when performing a set difference.
AI-generated content may contain errors. Please verify critical information