Uno hipérbola tiene uno de sus focos en el punto F1(10,0) y el segmento transversal mide 16 u, y su centro está en el origen. Encontrar la ecuación canónica?
Understand the Problem
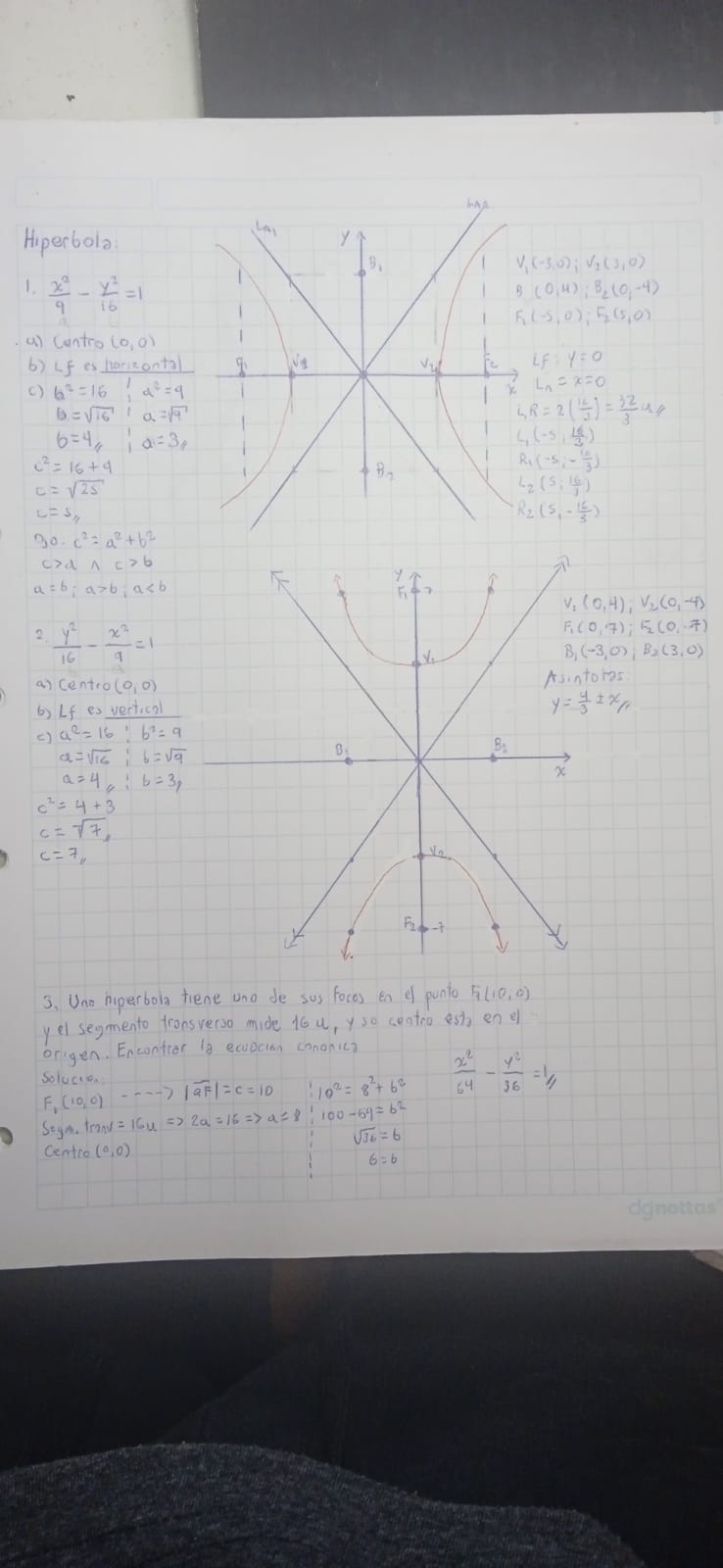
La pregunta se centra en analizar hipérbolas, incluyendo su ecuación canónica, características y elementos principales. Se presentan gráficos y se especifican condiciones como el centro, focos y ejes.
Answer
$$ \frac{x^2}{64} - \frac{y^2}{36} = 1 $$
Answer for screen readers
La ecuación canónica de la hipérbola es: $$ \frac{x^2}{64} - \frac{y^2}{36} = 1 $$
Steps to Solve
- Identificar los elementos de la hipérbola
La hipérbola dada tiene un foco en $F_1(10,0)$ y su centro en el origen $(0,0)$. La distancia entre el centro y un foco se denota como $c$, así que aquí $c = 10$.
- Determinar la longitud del eje transversal
Se nos dice que el segmento transversal mide $16u$, lo que significa que $2a = 16$. Por lo tanto, podemos encontrar $a$ como: $$ a = \frac{16}{2} = 8 $$
- Usar la relación entre $a$, $b$ y $c$
Utilizamos la relación: $$ c^2 = a^2 + b^2 $$
Sustituyendo los valores que tenemos: $$ 10^2 = 8^2 + b^2 $$
- Resolver para $b$
Calculamos $b^2$: $$ 100 = 64 + b^2 $$
Restando 64 de ambos lados: $$ b^2 = 100 - 64 = 36 $$
Tomando la raíz cuadrada: $$ b = \sqrt{36} = 6 $$
- Escribir la ecuación canónica de la hipérbola
La ecuación canónica de una hipérbola con el centro en $(0,0)$ y eje horizontal es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Sustituyendo $a^2$ y $b^2$: $$ \frac{x^2}{64} - \frac{y^2}{36} = 1 $$
La ecuación canónica de la hipérbola es: $$ \frac{x^2}{64} - \frac{y^2}{36} = 1 $$
More Information
Esta hipérbola está orientada horizontalmente, con focos en $F_1(10,0)$ y $F_2(-10,0)$, donde $a = 8$ y $b = 6$. La relación entre $a$, $b$ y $c$ es crucial para determinar la ecuación de la hipérbola.
Tips
- Olvidar la relación $c^2 = a^2 + b^2$: Es esencial usar esta relación para encontrar $b$.
- Confundir los ejes de la hipérbola: Asegúrate de identificar correctamente si es horizontal o vertical.