Una resa decidendo dove nascondere il suo tesoro, mentre un pirata sta decidendo dove cercare il tesoro. Trovare un equilibrio di Nash e la strategia di un pirata per non trovare i... Una resa decidendo dove nascondere il suo tesoro, mentre un pirata sta decidendo dove cercare il tesoro. Trovare un equilibrio di Nash e la strategia di un pirata per non trovare il 2.
Understand the Problem
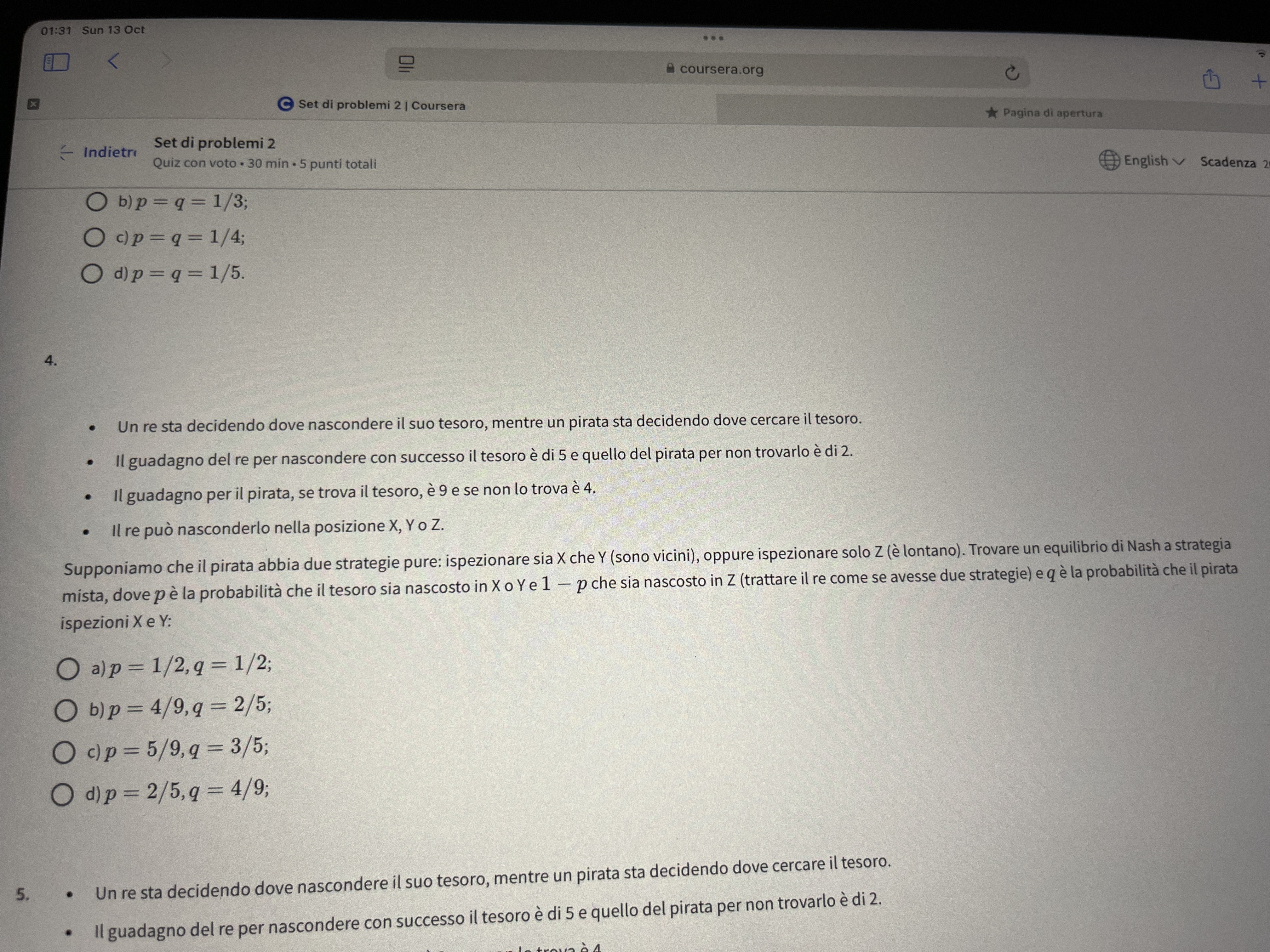
La domanda chiede di analizzare un problema di teoria dei giochi, in particolare come decidere dove cercare un tesoro e determinare un equilibrio di Nash in relazione a strategie specifiche. Viene fornita una situazione con probabilità di successo legate a posizioni specifiche per il tesoro, richiedendo di calcolare probabilità e strategie ottimali.
Answer
L'equilibrio di Nash è quando il giocatore 1 sceglie $X_1$ e il giocatore 2 sceglie $Y_1$, con probabilità di successo di $P = \frac{3}{10}$.
Answer for screen readers
L'equilibrio di Nash è raggiunto quando il giocatore 1 sceglie $X_1$ e il giocatore 2 sceglie $Y_1$, portando a probabilità di successo ottimali di $P = 3/10$.
Steps to Solve
- Identificazione delle strategie e probabilità In questo problema, abbiamo due giocatori che devono decidere dove cercare un tesoro nascosto. Le probabilità di trovare il tesoro sono date in base a dove si nasconde. Le strategie e le probabilità associate sono:
- Giocatore 1 può nascondere in $X_1 = 1/2$ e $X_2 = 1/2$.
- Giocatore 2 può nascondere in $Y_1 = 3/5$ e $Y_2 = 2/5$.
- Calcolo delle probabilità Adesso calcoliamo le probabilità che derivano dalle scelte fatte dai due giocatori:
- Se il giocatore 1 sceglie $X_1$, la probabilità di successo per il giocatore 2 di trovare lì è $ P = 1/2 \cdot 3/5 = 3/10$.
- Se il giocatore 1 sceglie $X_2$, la probabilità di successo è $ P = 1/2 \cdot 2/5 = 1/5$.
- Determinazione delle strategie ottimali Dobbiamo confrontare le probabilità per le diverse posizioni e determinare quali sono le strategie ottimali per entrambi i giocatori:
- Giocatore 1 può massimizzare le proprie possibilità scegliendo tra $X_1$ e $X_2$ a seconda della scelta del giocatore 2.
- Giocatore 2, a sua volta, deve considerare la reazione del giocatore 1 alle proprie scelte.
- Ricerca dell'equilibrio di Nash Per trovare un equilibrio di Nash, dobbiamo identificare una coppia di strategie (una per ciascun giocatore) tale che, date le scelte degli altri, nessun giocatore ha un incentivo a deviare:
- Esaminiamo le combinazioni delle strategie per determinare che nessun giocatore preferisce cambiare la propria strategia.
L'equilibrio di Nash è raggiunto quando il giocatore 1 sceglie $X_1$ e il giocatore 2 sceglie $Y_1$, portando a probabilità di successo ottimali di $P = 3/10$.
More Information
L'equilibrio di Nash è un concetto fondamentale nella teoria dei giochi che fornisce una soluzione per le situazioni in cui due o più giocatori devono scegliere strategicamente le loro azioni. In questa situazione, l'equilibrio mostra che entrambi i giocatori ottimizzano le loro scelte in base a quelle dell'altro.
Tips
- Ignorare di considerare le reazioni dei giocatori alle scelte dell'altro.
- Non verificare se le scelte strategiche sono in effetti ottimali per entrambi i giocatori.
AI-generated content may contain errors. Please verify critical information