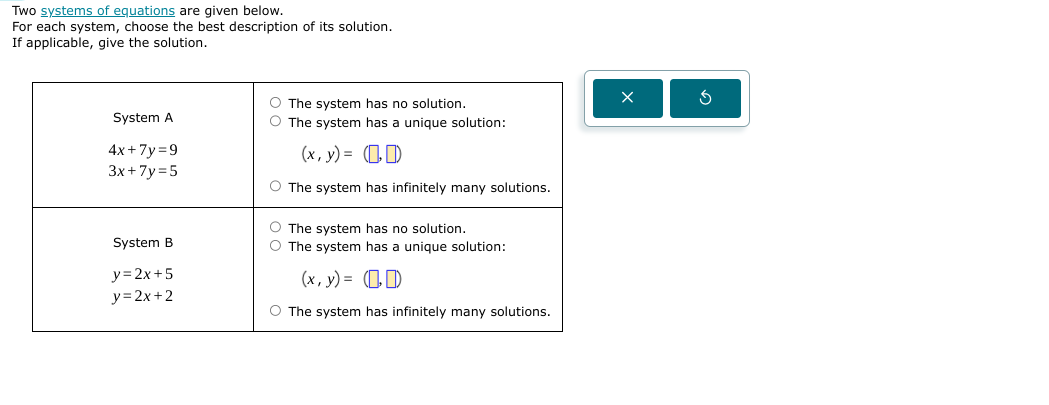
Two systems of equations are given below. For each system, choose the best description of its solution. If applicable, give the solution.

Understand the Problem

The question is asking to analyze two systems of linear equations to determine the nature of their solutions, whether they have no solution, a unique solution, or infinitely many solutions.

Answer

- System A: $(4, -1)$; System B: No solution.

Steps to Solve

Analyzing System A
- The equations are $4x + 7y = 9$ and $3x + 7y = 5$.
- To see if there is a unique solution, we can subtract these two equations: $$(4x + 7y) - (3x + 7y) = 9 - 5$$
- Simplifying gives: $$x = 4$$
- Now substitute $x = 4$ back into one of the original equations, say $4x + 7y = 9$: $$4(4) + 7y = 9 \implies 16 + 7y = 9 \implies 7y = -7 \implies y = -1$$
- The solution for System A is $(4, -1)$, which indicates a unique solution.
Analyzing System B
- The equations are $y = 2x + 5$ and $y = 2x + 2$.
- Both equations are in slope-intercept form, meaning they have the same slope of $2$.
- Since the y-intercepts differ ($5$ and $2$), the lines are parallel and will never intersect.
- Thus, System B has no solution.

System A: The system has a unique solution: $(x, y) = (4, -1)$.
System B: The system has no solution.

More Information

For System A, the two equations intersect at a point, meaning there is a unique solution where both equations are satisfied. In System B, the lines are parallel and do not intersect, indicating inconsistent equations and therefore no solution.

Tips

A common mistake is misinterpreting the nature of the equations. For System A, it is crucial to perform subtraction correctly to find the specific values of $x$ and $y$.
For System B, one might mistakenly assume that because both equations are linear, they must intersect; however, recognizing the different y-intercepts is key to identifying that they are parallel.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!