Two numbers are in the ratio 3:4. If HCF is 4, then what is the LCM?
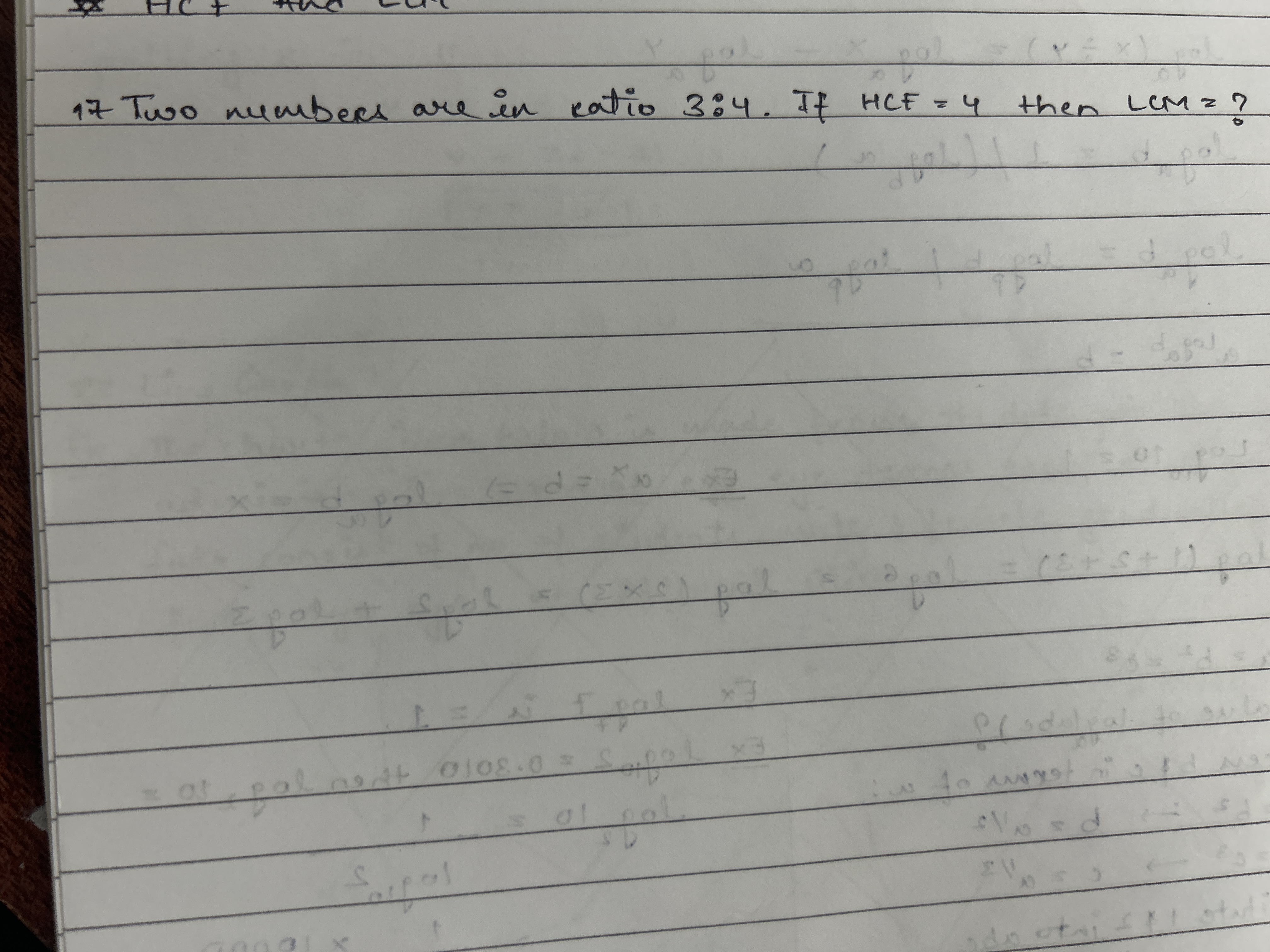
Understand the Problem
The question is asking for the LCM of two numbers given their ratio and HCF. The numbers are in the ratio 3:4 and the HCF is 4, and we need to use this information to find the LCM.
Answer
The LCM of the two numbers is $48$.
Answer for screen readers
The LCM of the two numbers is $48$.
Steps to Solve
- Understand the given information
The numbers are in the ratio $3:4$ and their HCF (Highest Common Factor) is $4$. We denote the two numbers as $a$ and $b$. Thus, we can express them as:
- $a = 3k$
- $b = 4k$ where $k$ is a common multiplier.
- Use the HCF to find the common multiplier
Since the HCF is given as $4$, we equate: $$ HCF(a, b) = k \cdot HCF(3, 4) $$
Since $3$ and $4$ are coprime, $HCF(3, 4) = 1$. Therefore: $$ k = 4 $$
- Calculate the two numbers
Now that we have $k$, we can calculate the numbers:
- $a = 3k = 3 \times 4 = 12$
- $b = 4k = 4 \times 4 = 16$
- Find the LCM using the relationship between LCM and HCF
The relationship between LCM and HCF states: $$ LCM(a, b) \times HCF(a, b) = a \times b $$
We can rearrange this to find LCM: $$ LCM(a, b) = \frac{a \times b}{HCF(a, b)} $$
- Plug in the values to calculate the LCM
Now we substitute the values of $a$, $b$, and HCF: $$ LCM(12, 16) = \frac{12 \times 16}{4} $$
Calculating this gives: $$ LCM(12, 16) = \frac{192}{4} = 48 $$
The LCM of the two numbers is $48$.
More Information
The LCM (Least Common Multiple) is useful in various applications such as finding common denominators in fractions, scheduling events, and many problems involving multiplication of integers. The numbers in this specific example illustrate the relationship between ratios and factors clearly.
Tips
- Not using the ratio correctly: It’s essential to express the numbers in terms of the ratio and the HCF properly.
- Incorrectly applying the LCM formula: Make sure to substitute HCF and product of numbers accurately.
AI-generated content may contain errors. Please verify critical information