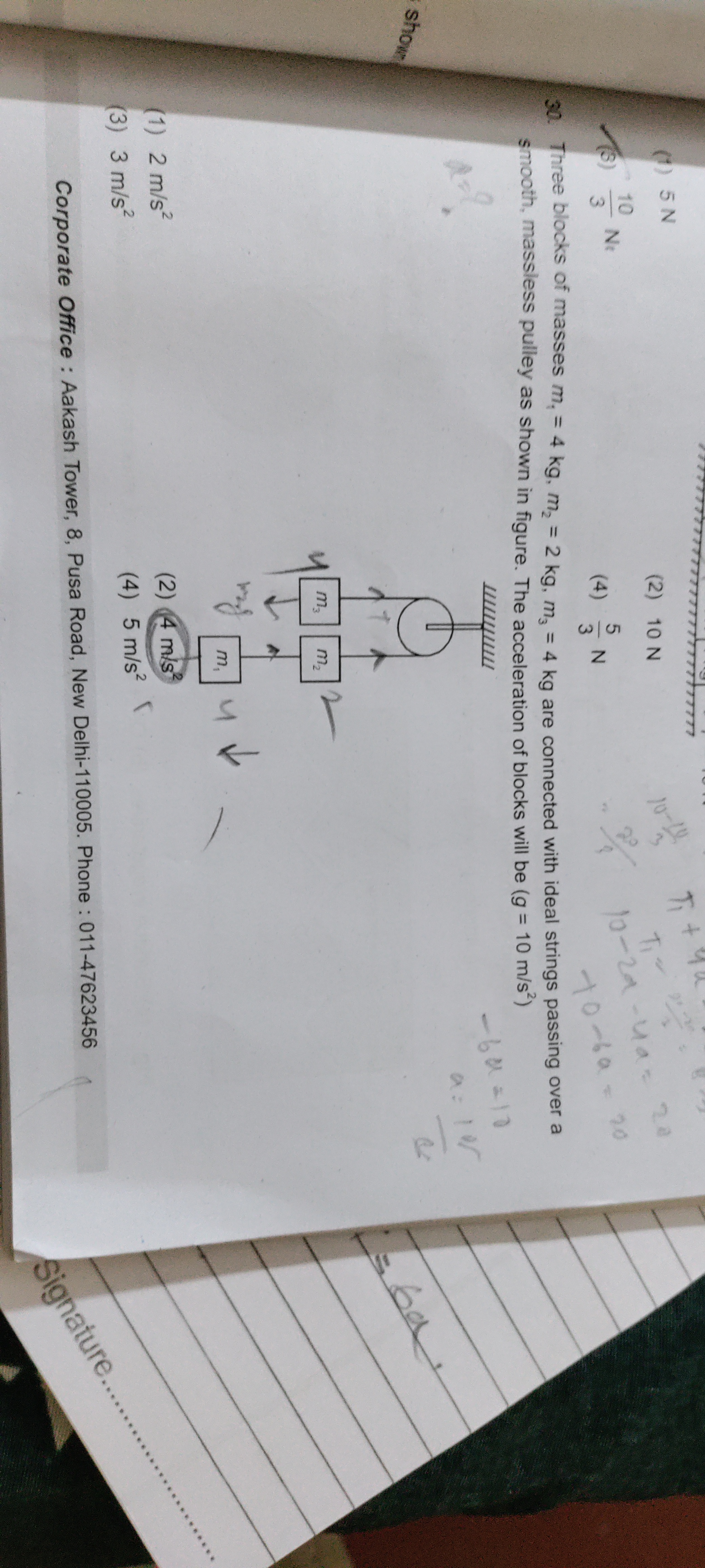
Three blocks of masses m1 = 4 kg, m2 = 2 kg, m3 = 4 kg are connected with ideal strings passing over a smooth massless pulley. What will be the acceleration of the blocks?

Steps to Solve

1. Identify the Forces Acting on Each Block

   The system has three blocks connected by ideal strings passing over a pulley.

   • For $m_1 = 4, \text{kg}$ (on the left): The force due to gravity is $F_g = m_1 g = 4 \times 10 = 40, \text{N}$, acting downwards.
   • For $m_2 = 2, \text{kg}$: The force due to gravity is $F_g = m_2 g = 2 \times 10 = 20, \text{N}$, acting downwards.
   • For $m_3 = 4, \text{kg}$ (on the right): The force due to gravity is the same as $m_1$, $F_g = 40, \text{N}$, acting downwards.

2. Apply Newton's Second Law

   Using Newton's second law, we write the equations for the blocks based on the forces acting on them.

   • For $m_1$:
     $$ T - m_1 g = -m_1 a $$ (where $T$ is the tension and $a$ is the acceleration).

   • For $m_2$:
     $$ T - m_2 g = -m_2 a $$

   • For $m_3$:
     $$ T - m_3 g = -m_3 a $$

   This gives us three equations.

3. Solve for Tension and Acceleration

   Combine the equations to eliminate $T$ and solve for the acceleration $a$ of the system.

   • From the second block's equation: $$ T = m_2 g + m_2 a $$ Substitute into the first block's equation:

   $$ m_2 g + m_2 a - m_1 g = -m_1 a $$

   Rearranging yields: $$ m_2 g - m_1 g = (m_1 + m_2) a $$

   Substitute the masses and solve for $a$.

4. Calculate the Result

   Substitute the values into the equation: $$ (20 - 40) = (4 + 2) a $$ Simplifying gives: $$ -20 = 6a $$ Thus: $$ a = -\frac{20}{6} \approx -3.33 , \text{m/s}^2. $$

5. Check for Direction and Units

   Since acceleration cannot be negative in this context, we conclude the acceleration's magnitude is: $$ a = 3.33 , \text{m/s}^2. $$